Distancias mínimas entre rectas y planos

La distancia mínima es siempre perpendicular a la(s) recta(s) y solo se encontrará en donde al menos una de las rectas aparezca como un punto. Para llevar a cabo esto, su visual debe ser paralela a la recta que aparece en verdadera forma y magnitud.

Sea la figura siguiente figura

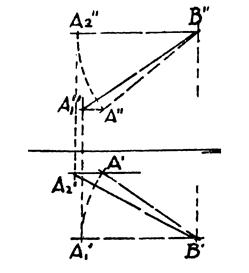
1º Introduzcamos un eje vertical que pase por el punto B’ y alrededor de él hagamos girar la AB hasta que se sitúe en el plano frontal que pasa por el eje. Con este giro obtendremos con las proyecciones A’1B’ y A”B”, hecha frontal, cuya longitud real entre los dos puntos se manifiesta en la segunda proyección.

2º Si efectuamos ahora, el giro alrededor de un eje de punta que pase por el punto B, haciendo girar la recta hasta que se sitúe en un plano horizontal que pase por el eje, la proyección vertical del punto A, describirá en el plano frontal un arco de círculo y la mencionada proyección se situará en A’2, como la recta resulta horizontal en esta posición B’A’ se manifiesta en verdadera magnitud.

Fuente: Apuntes de Geometría descriptiva de la Universidad de Londres