Método de las 2 fases
En esencia es igual al método de penalización, en que primero se introducen las variables artificiales al problema original
Sujeto a
Quedando como
Sujeto a
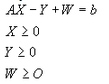
Donde W es el vector de variables artificiales con componentes 
. En la primera fase se resuelve el problema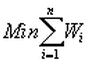
Sujeto a
La solución óptima de esta fase debe ser W = 0. Si al obtener las condiciones de optimalidad en esta fase, W > 0, el problema original no tiene solución.
Supóngase que la primera fase es óptima,W = 0 y que la base asociada a la tabla es B. En la segunda fase se aplica el método Simplex para resolver el problema
Min cX
Sujeto a
La solución óptima a esta segunda fase, es la solución óptima al problema original. Es importante observar que al empezar la segunda fase, todos los vectores de la base óptima correspondientes a la primera fase permanezcan unitarios.
Empléense operaciones matriciales elementales para restituir todos aquellos vectores que deben ser unitarios.
Fuente: Apunte de Investigación de Operaciones del Instituto Tecnológico de la Paz
