Paralelismo entre rectas y planos

Construir un plano paralelo a una recta dada a’b’ ab

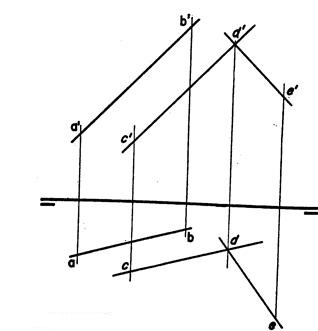.1º Constrúyase una recta tal como c’d’ cd paralela a la dada.

2º Por un punto cualquiera d’d de la recta c’d’ cd hágase pasa otra cualquiera d’e’ de. Estas dos rectas se cortan determinando un plano c’d’e’ cde que es paralelo a la recta.

El problema tiene infinidad de soluciones, tantas como rectas sean paralelas a la primera y para cada una de ellas tantas como otras que las cortan. Un plano es paralelo a una recta (fig 204) cuando contiene por lo menos una recta paralela a ella.

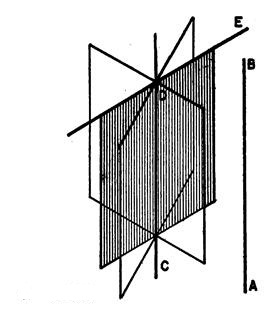
Fuente: Apuntes de Geometría descriptiva de la Universidad de Londres