Restricciones a las que está sometida la elección de las rectas soporte de las seis fuerzas
Cualquier sistema de fuerzas admite uno equivalente constituido por seis fuerzas cuyas rectas soporte fijamos con un elevado grado de arbitrariedad, en este apartado queremos analizar las restricciones a las que está sometida dicha elección.
La posibilidad de descomponer cualquier torsor de fuerzas aplicadas a un cuerpo rígido sobre una determinada base de rectas soporte está íntimamente relacionada con el problema de la ubicación de las ligaduras que inmovilizan este cuerpo de forma estricta (no superabundante).
Sean Pi (i=1,..6) seis puntos, uno para cada una de las mencionadas rectas soporte cuyos vectores directores son vi (i=1,..6), y sea Q un punto arbitrario. Consideremos los vectores:
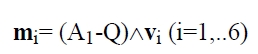
A partir de las parejas {vi, mi}, definimos unos vectores hexadimensionales:
El torsor se podrá descomponer en seis fuerzas de la forma:{Ai ,αiv1} (i=1,..6) si no es nulo el determinante de la matriz cuadrada (ma) de 6×6 elementos cuyas columnas son los seis hexavectores wi.
![]()
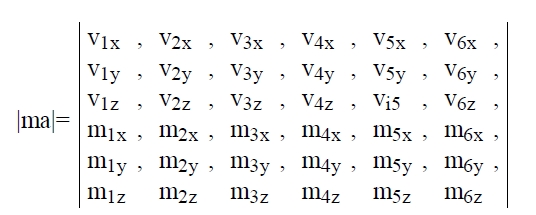
En efecto: si el torsor del sistema que queremos descomponer es: τ={B, R, M [B]} la equivalencia entre el sistema cuyo torsor queremos descomponer y el formado por las seis fuerzas buscadas se expresa de la siguiente manera:
Representación de las fuerzas
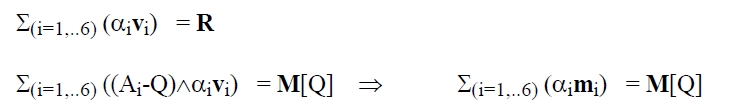
Si definimos el hexavector cuyas componentes son las de la pareja:
Ω={R, M[Q]} las dos ecuaciones de equivalencia se pueden sintetizar en la ecuación con vectores hexadimensionales:
![]()
cuya expresión en forma matricial es:
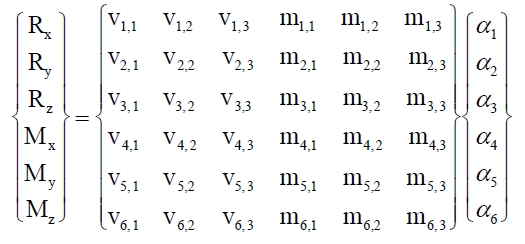
Esta ecuación admite solución única para cualquier torsor (cualquier sistema Ω) cuando no es nulo el mencionado determinante de la matriz ma.
|ma|≠0
Fuente: Apuntes de Física del Departamento de Física Aplicada
