Correspondencia asociativa por conjuntos

En la correspondencia asociativa por conjuntos las líneas de Mc se divide en v=2d conjuntos con k líneas/conjunto o vías cada uno. Se cumple que el número total de marcos de bloque (líneas) que tiene la caché m = v*k. Un bloque Bj de Mp se puede ubicar sólo en el conjunto Ci de Mc que cumple la siguiente relación i = j mod v.

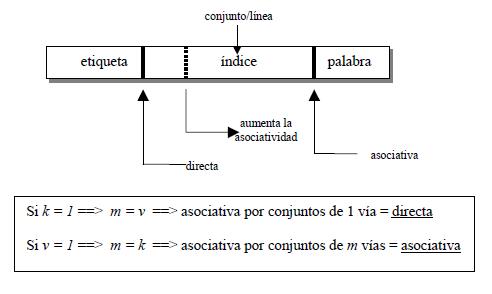
Interpretación de una dirección física en correspondencia asociativa por conjuntos:

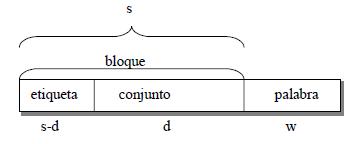
En este caso la etiqueta tendrá s – d bits para poder diferenciar a cada uno de los bloques de Mp que pueden ubicarse en el mismo conjunto de Mc. El directorio caché en correspondencia asociativa por conjuntos contendrá, pues, un registro de s – d bits por cada conjunto de líneas de Mc.

El esquema lógico de acceso a una caché de correspondencia asociativa por conjuntos se muestra en la siguiente figura:

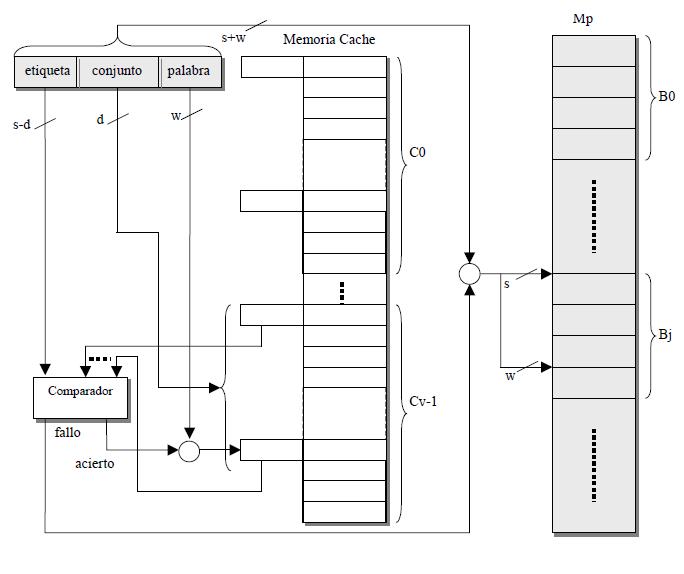
Una Mc de correspondencia asociativa por conjuntos de v vías se puede implementar como k módulos de correspondencia directa en paralelo cada uno con v líneas. Los conjuntos lo formarían las líneas que ocupan idéntica posición en cada módulo:

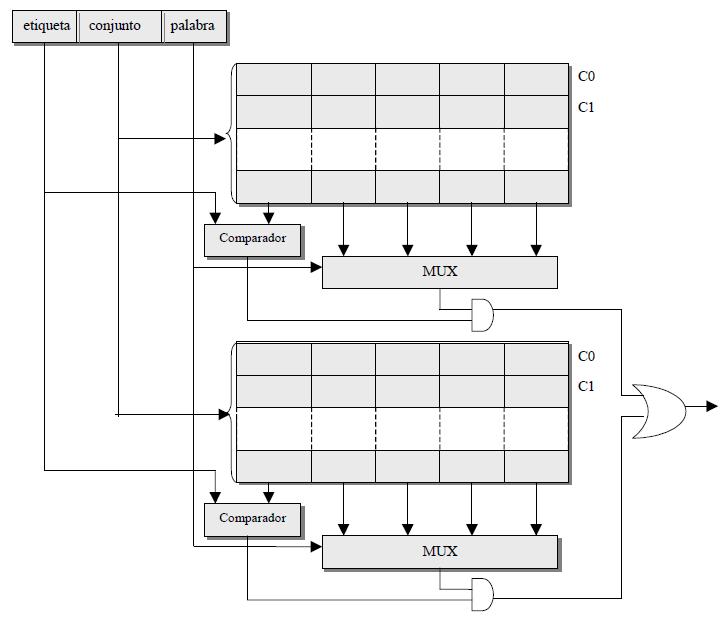
Si dibujamos Mp dividida en zonas consecutivas de tamaño 32 KB (con tantos bloques como conjuntos tiene Mc) para facilitar la correspondencia de los bloques de Mp y los marcos de bloque de Mc, podremos representar fácilmente parte de un posible contenido de Mc con correspondencia asociativa por conjuntos de dos vías en un instante determinado para el ejemplo anterior.

k = 2 => v = m/k = 2r/2 = 214/2 = 213 => d = 13
w = 2
s = 22 => s -d = 9

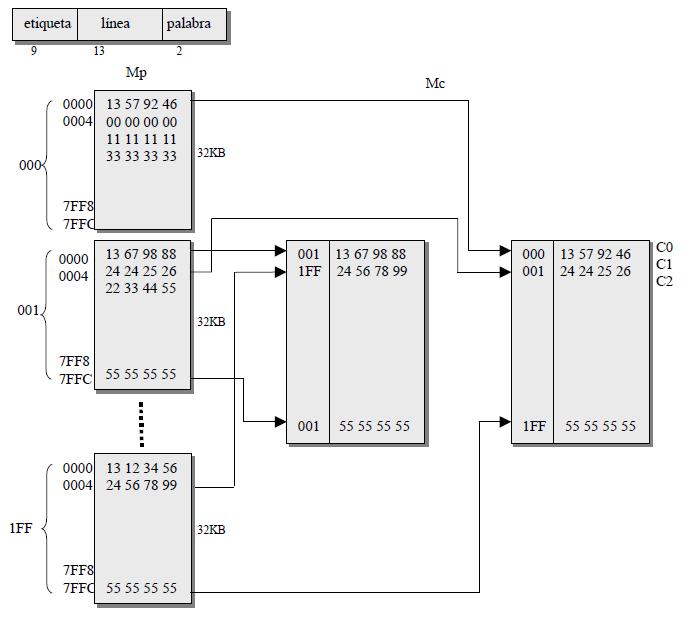
Las tres funciones de correspondencia se pueden ver en realidad como una sola, la asociativa por conjunto, siendo las otras dos correspondencias casos extremos de ella:

Fuente: Estructura de Computadores, Facultad de Informática, UCM