Ecuación de la parábola con vértice en el origen y eje que coinciden con alguno de los ejes coordenados

Una parábola es un conjunto de puntos sobre el plano tales que la distancia de cualquiera de esos puntos a un punto fijo, llamado foco, es igual a la distancia (perpendicular) de ese mismo punto a una recta fija llamada directriz.

En la figura 4.11 el punto P(x, y) es un punto cualquiera sobre la parábola, el foco F tiene por coordenadas ( p,0) y la directriz l tiene por ecuación x = – p . El vértice de esta parábola es el punto 0 de coordenadas (0,0) y el eje de la parábola coinc ide con la parte positiva del eje x; un poco más adelante entenderás a fondo la relación que la directriz tiene con parábola.

Parábola con vértice en el origen

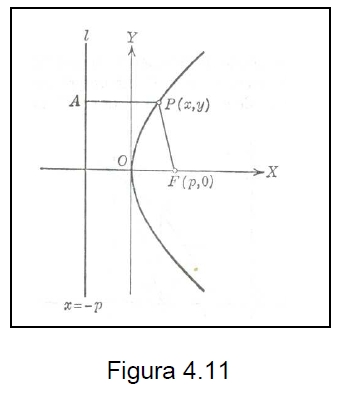
La definición de la parábola establece que la distancia AP es igual a la distancia PF para cualquier punto de la parábola.

La ecuación de la parábola se obtiene al calcular (de manera general) la distancia de cualquiera de sus puntos al foco, y a la directriz, e igualarlas.

Esta derivación de la ecuación de la parábola puedes leerla en el libro de Geometría Analítica, de Lehmman, citado en la bibliografía.

La ecuación de la parábola con vértice en el origen, y eje que coincide con el eje X, es

y ²  = 4 px ,

en donde el foco es el punto ( p,0) , y la ecuación de la directriz es x = – p . Si p0 la parábola se abre hacia el lado positivo del eje, si p < 0 , la parábola se abre hacia la parte negativa del eje.

Parábola con vértice en el origen (a)

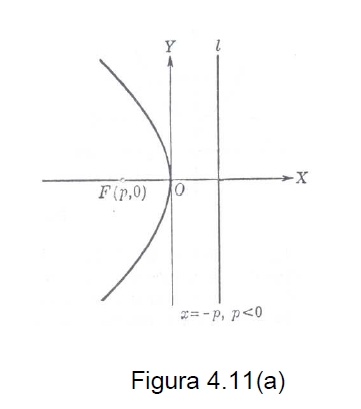
La parábola puede tener distintas orientaciones, es to es, su eje puede coincidir con el eje X y sus brazos abrirse hacia la parte positiva del eje x (figura 4.11), o abrirse hacia la parte negativa del eje (figura 4.11(a)); también puede ocurrir que el eje de la parábola coincida con el eje Y, y sus brazos se abran hacia la parte positiva del eje y (figura 4.12(a)), o hacia la parte negativa (figura 4.12(b)).

Parábola con distintas orientaciones

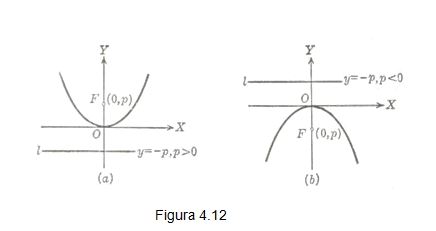
Cuando la parábola tiene vértice en el origen y su eje coincide con el ejeY su ecuación es x ²  = 4 py en donde el foco es el punto (0, p) , y la ecuación de la directriz es y = – p . Si p0 la parábola se abre hacia el lado positivo del eje, si p0, la parábola se abre hacia la parte negativa del eje.

Ejemplo:

Hallar la ecuación de la parábola, las coordenadas de su foco, y la ecuación de su directriz, si la parábola tiene vértice en el origen, pasa por el punto (4, -2) y su eje coincide con el eje Y.

Solución:

Como el problema nos dice que el eje de la parábola coincide con el eje Y, su ecuación tendrá la forma x ²  = 4 py.

Como pasa por el punto (4,-2), sabemos que se abre hacia el lado negativa del eje, además este punto debe satisfacer la ecuación, así que si sustituimos el punto en esta última hallaremos el valor de p.

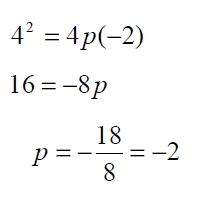
La ecuación de la directriz es y = – p , y el foco (0, p) , sustituyendo p = -2  se obtiene y = -(-2) = 2

directriz  y = 2  y foco (0,-2).

Finalmente, la ecuación de la parábola es

Fuente: Apunte de matemáticas básicas de la UNIDEG.