Enlaces en geometría descriptiva

Enlaces son las uniones armónicas por medio de tangencias entre distintas figuras.

Para resolver problemas de tangencia hay que tener presente las dos propiedades fundamentales de las tangencias:

– El radio que pasa por el punto de tangencia es perpendicular a la recta tangente.

– Los centros de dos circunferencias tangentes están alineados con el punto de tangencia.

Enlace de dos rectas

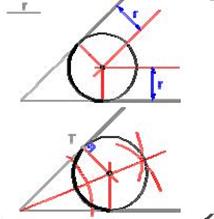
Para definir el problema se necesita conocer el radio o un punto de tangencia. Si conocemos el radio, trazamos paralelas a las rectas dadas, a una distancia igual al radio, obteniendo el centro del arco en su intersección.

Los puntos de enlace se hallan trazando perpendiculares por el centro del arco a las rectas tangentes.

Si el dato es el punto de tangencia, la perpendicular trazada por el punto de tangencia a la recta, y la bisectriz del ángulo que forman, se cortan en el centro del arco.

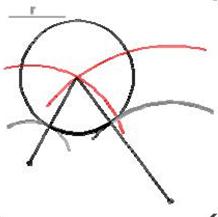
Enlace de dos arcos

Dándonos el radio, las circunferencias concéntricas de radios iguales a la suma y diferencia, determinan los centros del arco de enlace. Sabemos que los puntos de enlace están alineados con los centros.

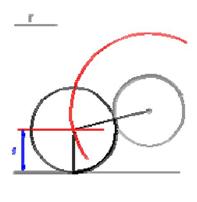
Enlace de arco y recta

Las paralelas a la recta a una distancia igual al radio dado y las circunferencias concéntricas de radios la suma y diferencia, determinan los centros.
Fuente: Apuntes de Geometría descriptiva de la Universidad de Londres