Ensayo de tracción

Cuando un material está sometido a fuerzas sobre una cara determinada las fuerzas que actúan se pueden descomponer en 2 tipos: una fuerza normal a la cara y otra fuerza tangencial. La fuerza normal (FN) si es de “estiramiento” del material se conoce como fuerza de
tracción y si es de aplastamiento como fuerza de compresión.

La fuerza tangencial a la cara (Ftg) se conoce como fuerza de cizalladura o cizallamiento. La fuerza de tracción se considera, en general, positiva y la de compresión negativa.

El ensayo de tracción consiste en estudiar la respuesta del material frente a fuerzas de tracción. Este ensayo permite caracterizar propiedades del material, pero éstas no son directamente aplicables a piezas concretas porque cada pieza, dependiendo de su diseño, puede presentar particularidades específicas.

Para realizar el ensayo el ensayo de tracción se utilizan muestras (probetas), generalmente cilíndricas y alargadas. Suelen presentar la siguiente forma:

– Mediante una máquina de ensayos se fija el extremo inferior de la probeta y al extremo superior se le va aplicando, en forma continua y progresiva, fuerzas de tracción crecientes hasta que se produce la rotura de la probeta.

Durante el ensayo se van midiendo la distancia entre dos puntos, A y B situados en una generatriz del cuerpo cilíndrico de la probeta y se van tomando pares de valores: fuerza aplicada vs. longitud entre los puntos. Se observa que a medida que la probeta es más gruesa se deforma menos al aplicar una determinada fuerza.

Por esto esto, la respuesta del material frente a la fuerza aplicada va a depender del espesor de la muestra que se considere, y para evitar esta dependencia, en lugar de considerar como parámetro la fuerza, se considera la carga de tracción, definida como Análogamente, si el material al que se le aplica una carga es de 1 metro de longitud, se producirá un aumento de su longitud inicial del doble que si fuese de medio metro.

Para evitar esta dependencia del comportamiento del material en función de la longitud de la probeta utilizada, no se utilizan incrementos de longitud como parámetros (lo que se alarga A-B), sino deformaciones, que se definen en la forma:

Análogamente, si el material al que se le aplica una carga es de 1 metro de longitud, se producirá un aumento de su longitud inicial del doble que si fuese de medio metro. Para evitar esta dependencia del comportamiento del material en función de la longitud de la probeta utilizada, no se utilizan incrementos de longitud como parámetros (lo que se alarga A-B), sino deformaciones, que se definen en la forma:

A veces se emplean las deformaciones en %:

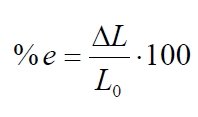
Si se representan en una gráfica las deformaciones (en el eje de abscisas) a que dan lugar las cargas de tracción, se obtiene una curva que se conoce como curva de tracción, y que en general presenta una forma análoga a la de la figura:

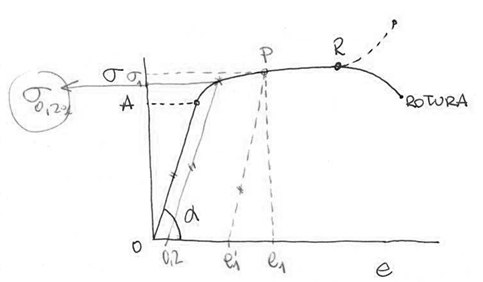
En un primer tramo OA existe linealidad entre la carga y la deformación. En este tramo se cumple que:

cte e

Esa constante, que es tg α, se conoce como módulo de Young o módulo de elasticidad, y se representa por E:

E e

El valor de E es ya una característica importante del material que permite determinar la deformación longitudinal que sufrirá este cuando se le aplique una carga dada, siempre que ésta sea inferior a A.

La carga correspondiente a A se conoce como límite elástico teórico. A partir del punto A el material presenta un comportamiento diferente.

Dentro de la zona de comportamiento elástico (cargas inferiores a A) si se retira la carga, el material recupera sus formas y dimensiones originales.

A partir del punto A se dice que el material se comporta plásticamente, y en esta zona plástica el material queda con σ deformaciones permanentes. Si una carga dentro σde la zona plástica ( 1) produce una deformación e1, al retirar la carga 1 el material recupera elásticamente una cierta parte de sus dimensiones originales (en nuestro ensayo, de su longitud inicial) pero queda deformado permanentemente con una deformación e’1.

Es decir, el material tiene una cierta recuperación elástica (cuyo valor es el del tramo e1-e’1) y queda con una deformación permanente 0-e’1. Para determinar la recuperación elástica, es decir, para determinar el punto e’1, se parte del punto representativo P en la curva y se traza por él una paralela a 0A, que cortará en el eje de abscisas en el punto e’1 a determinar.

El punto A (límite elástico teórico) es imposible de determinar. Por tanto, se suele utilizar el límite elástico práctico, que en el caso de ingeniería suele ser aquel que produce una deformación permanente del 0,2%; se determina haciendo pasar por la abscisa de 0,2% una paralela al tramo 0A y la ordenada del punto de corte de esta paralela con la curva de tracción será la carga correspondiente a una deformación permanente de 0,2%,σcarga que se define como límite elástico del 0,2% y se representa por “ 0,2%”. Existen valores del límite elástico para el 0,3%, 0,4%,…

En la zona plástica de la curva hay un máximo que corresponde al punto R y cuya carga se representa como “R” y que se conoce como resistencia a la tracción; es la carga máxima que soporta un material cuya sección original es S0. A partir de este valor, el material puede continuar deformándose aunque disminuya algo la fuerza aplicada y, finalmente, acabará rompiéndose.

En la zona plástica, a partir de unas determinadas cargas se observa que la probeta, a medida que ha ido alargándose se ha ido estrechando simultáneamente (disminuyendo su sección). Sufre un estrangulamiento localizado en una zona, que a partir de su aparición se desarrolla rápidamente.

Este fenómeno, que se conoce como estricción, es característic de materiales plásticos, y sobre esa zona se produce la rotura. Una vez está la probeta rotase encajan los dos fragmentos en la zona de rotura y se mide la longitud entre A y B después de la rotura, así como la sección de la zona más estrecha de la probeta.

Fuente: Apuntes de Ciencia de Materiales. Ingeniería Química – Universidad de Huelva