En el desarrollo que a continuación se presenta se usa la siguiente forma de la programación lineal, denominada forma canónica.
Máx Z = cX
Sujeto a
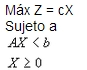
Cualquier otra forma es equivalente a la anterior. Esta equivalencia se prueba fácilmente por medio del uso de cualquiera de las siguientes 5 reglas.
Regla 1
Maximizar cX es equivalente a Minimizar –cX
Minimizar cX es equivalente a Maximizar –cX
Ejemplo:
es equivalente a
Es equivalente a
es equivalente a
Regla 2
La desigualdad 
es equivalente a la desigualdad 
La desigualdad 
es equivalente a la desigualdad 
Ejemplo:
es equivalente a
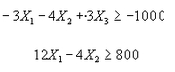
es equivalente a
Regla 3
Toda igualdad de la forma 
, puede descomponerse como la intersección de dos desigualdades y
Ejemplo:
es equivalente a
Regla 4
Toda desigualdad de la forma puede convertirse en igualdad mediante la adición de un vector Y, llamado de holgura. El vector columna Y tiene m componentes, todas ellas no negativas, es decir
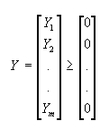
Toda desigualdad de la forma
puede convertirse en igualdad mediante la resta de un vector Z, llamado superfluo. El vector columna Z, tiene m componentes, todas no – negativas, es decir:
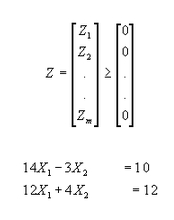
Ejemplo:
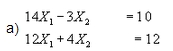
es equivalente a
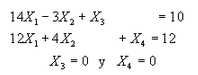
Donde el vector de holgura es
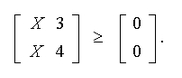
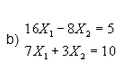
es equivalente a
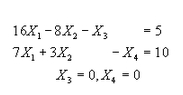
Donde el vector de exceso o superfluo es
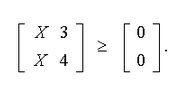
Regla 5
Una variable no restringida, o sea aquella que puede tomar toda clase de valores positivos, cero y negativos puede escribirse como la diferencia de dos variables no – negativas.
Fuente: Apunte de Investigación de Operaciones del Instituto Tecnológico de la Paz