Interpretación de las tablas de radiación

La cantidad de energía recibida del Sol (radiación solar) y la demanda diaria de energía son los dos factores que marcan la pauta para diseñar un sistema solar fotovoltaico.

El consumo eléctrico del equipo receptor queda determinado por la potencia eléctrica consumida multiplicada por las horas de funcionamiento a que va a estar sometido dicho equipo. Restaría, pues, analizar la potencia recibida del Sol en el lugar de ubicación para poder calcular el número de módulos fotovoltaicos necesarios para que se equipare globalmente la potencia producida a la consumida.

La elección de los datos de radiación solar dependerá directamente de la situación de la instalación, así como de las condiciones meteoroló gicas predominantes y particulares de cada lugar.

Es de suma importancia considerar las condiciones particulares del lugar de la instalación, recogiendo datos referidos a nieblas, precipitaciones frecuentes, nieve y altura que puede alcanzar ésta, temperaturas máximas, mínimas y medias, etc., factores todos a tener en cuenta a la hora de calcular el sistema.

Los datos ofrecidos en las tablas de radiación suelen ser medias de medidas realizadas en varios años, de tal forma que se ofrecen valores promediados de años buenos, regulares y malos meteorológicamente hablando, hecho que nos asegura una mayor fiabilidad en dichos datos.

Lo mismo ocurre con los datos mensuales de las tablas de radiación, ya que durante el transcurso de un mes se pueden presentar condiciones meteorológicas prolongadas de lluvias, nieves, días nublados, tiempo seco y claro, que pueden afectar a los cálculos mensuales de radiación solar. Sin embargo, estos fenómenos se promedian a lo largo de varios años de toma de datos, haciéndolos muy fiables a partir de medias calculadas durante cinco o más años.

Las unidades de medición de energía solar que comúnmente se usan son el langley (caloría por centímetro cuadrado) y, con más frecuencia, el kilojulio por metro cuadrado. Otra unidad es la Btu por metro cuadrado (o por pulgada cuadrada), pero ésta es más utilizada en los diseños de colectores térmicos que en los fotovoltaicos.

– Radiación mensual

El ángulo de inclinación más idóneo para obtener la máxima radiación en un determinado mes. Esto es bastante común en los cálculos fotovoltaicos, ya que muchos sistemas deben diseñarse para soportar las peores condiciones de insolación, asegurando la alimentación de la carga.

Supongamos que deseamos obtener la media máxima de radiación en los meses más desfavorables y definir el ángulo al cual deben de inclinarse los módulos fotovoltaicos. Para ello, buscaremos en las columnas de noviembre, diciembre y enero, que resultan ser las más homogéneas en toda la gama de ángulos respecto al valor de radiación.

Si observamos detenidamente, tanto octubre como febrero incrementan notablemente su valor, por lo cual, si los incluyéramos, la media de radiación a calcular se vería desviada y, por lo tanto, podría damos un dato más elevado pero menos fiable para un cálculo fotovoltaico.

El paso siguiente consiste en comparar dónde se producen las máximas radiaciones en los tres meses antes indicados. Para esto, observaremos que los valores mayores para noviembre y enero se consiguen a un ángulo de 60° y para el mes de diciembre a 65°, pero con una variación de tan sólo 60 kJ/m2, valor totalmente despreciable, por lo que podemos establecer como ángulo más idóneo el de 60°, y una radiación media en los meses más desfavorables de:

(Nov. + Dic. + Ene.)/3 = (12430+ 12646+ 11206)/3 = 12094 kJ/m2

Observemos que los valores del mes de noviembre y diciembre superan la media y tan sólo enero presenta una desviación del 7.3%, por lo cual este dato de radiación podría ser utilizado, comprobando que el déficit producido en enero puede ser absorbido por la batería de acumuladores.

Dicho déficit sería rápidamente compensado en el mes siguiente, ya que la radiación solar aumenta en más de 2000 kJ/m2. Los valores antes expresados y los ofrecidos en las tablas corresponden a valores medios diarios de cada uno de los días del mes.

Puede darse también el caso de sistemas fotovoltaicos que se utilicen durante uno o dos meses al año, por ejemplo en verano, y deseemos encontrar la máxima radiación y el ángulo de inclinación.

Para ello, igual que en el caso anterior, tendremos que buscar el mes de mayor insolación, que resulta ser julio, y el ángulo de inclinación más idóneo sería el de 10° sobre la horizontal, produciéndose una radiación de 26072 kJ/m2 en estas condiciones.

Como conclusión, se puede decir que para obtener las mayores radiaciones de los meses más desfavorables, los ángulos que debemos utilizar rondarán los 60° para el territorio de la península, y por el contrario, las mayores radiaciones de los meses estivales serán con ángulos pequeños.

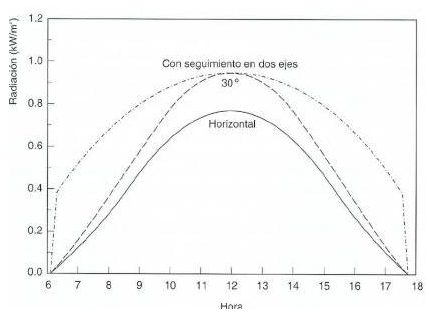
– Radiación anual máxima

Puede darse el caso de que se necesite el valor más elevado de radiación a lo largo de un año. Para ello bastará buscar en la tabla anterior el mayor valor en la columna correspondiente a los totales, que en este ejemplo se sitúa en 6312798 kJ/m2 por año, lo que supone 17295.3 kJ/m2 por día, y que corresponde a un ángulo de 30° sobre la horizontal.

En la práctica estos datos suelen ser usados pocas veces, dado que las instalaciones, normalmente, tienen un consumo muy equilibrado día a día, como para diseñar el sistema basándose en este parámetro, pues si lo analizamos bien, vemos que sólo los meses de abril, mayo, junio, julio, agosto y septiembre superarían el valor promedio de 17295.3 kJ/m2, lo que nos indica que deberíamos disponer de un acumulador capaz de suministrar energía durante seis meses al año y esto, en muchos casos, no resulta ni técnica ni económicamente viable.

– Máxima radiación mensual

Tampoco es muy habitual el que se diseñen sistemas que varíen el ángulo mensualmente para obtener la máxima radiación y aprovechar mejor el sol en cada uno de los meses.

Tan sólo en los sistemas de seguimiento se utiliza esta técnica, interesante para grandes despliegues de paneles fotovoltaicos, pues es totalmente necesario el tener un servicio de mantenimiento, que en esos casos quedaría justificado, pero no normalmente en una pequeña instalación.

En la tabla siguiente se muestran las radiaciones mensuales máximas y los ángulos en los cuales se producen.

Si nos fijamos en los ángulos, observaremos que a medida que se acerca el verano, la radiación máxima se produce a un ángulo más pequeño debido a la altura que va tomando el Sol. Lo contrario ocurre en el invierno, cuando sus rayos no son perpendiculares a la superficie terrestre, sino mucho más inclinados.

– Radiación diaria

Si observamos la tabla de radiación solar (potencia incidente) podemos sacar varias conclusiones como, por ejemplo, la hora a la cual se va a producir la primera incidencia de radiación sobre el panel, así como su valor, y el final de radiación y principio de la noche.

Estos datos pueden servir para determinar, por ejemplo, el tiempo de funcionamiento a lo largo de los meses de un sistema de balizaje, o evaluar la producción hora por hora de un módulo fotovoltaico a lo largo del día.

Si nos fijamos en los ángulos, observaremos que a medida que se acerca el verano, la radiación máxima se produce a un ángulo más pequeño debido a la altura que va tomando el Sol. Lo contrario ocurre en el invierno, cuando sus rayos no son perpendiculares a la superficie terrestre, sino mucho más inclinados.

– Radiación diaria

Si observamos la tabla de radiación solar (potencia incidente) podemos sacar varias conclusiones como, por ejemplo, la hora a la cual se va a producir la primera incidencia de radiación sobre el panel, así como su valor, y el final de radiación y principio de la noche.

Estos datos pueden servir para determinar, por ejemplo, el tiempo de funcionamiento a lo largo de los meses de un sistema de balizaje, o evaluar la producción hora por hora de un módulo fotovoltaico a lo largo del día.

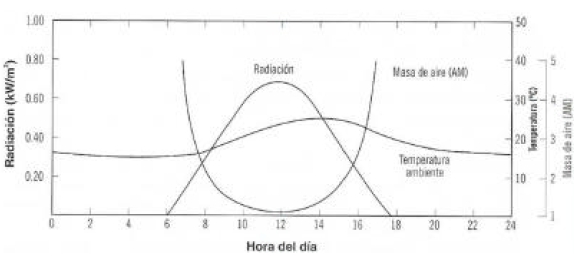
Este último caso puede ser llevado a un diagrama como el de la figura, observando que se produce una curva en forma de campana, donde en su parte más elevada se produce el máximo de radiación al incidir el sol frontalmente al módulo solar. Este punto coincide también con el pico de producción eléctrica de dicho módulo.

Normalmente, todas las tablas de radiación están expresadas en kJ/m2. No obstante, se pueden encontrar algunas cuyas unidades sean los langleys (cal/cm2), o bien el Btu-hora/pie2 (Btu h/ft2). Estableceremos las diversas correspondencias entre todas las unidades:

100 mW /cm2 = 317 Btu.h/ft2 = 86 langleys/h

Dado que una caloría es igual a 4.186 julios, tendremos que: 1 julio = (1/4.186) cal = 0.24 calorías

1 kJ/m2 = (l kJ) / (l0-4 cm2) = 10-4 kJ/cm2

1 kJ/m2 = 0.1 julios/cm2

0.1 julios/cm2 = 0.1 x 0.24 cal/cm2

Resumiendo: 1 kJ/m2 = 0.024 cal/cm2, o sea 1 kJ/m2 = 0.024 langleys

Luego, bastará multiplicar los valores en kJ/m2 por el factor 0.024 para obtener directamente el valor en langleys.

Quizás una de las conversiones más importantes es la que relaciona el valor de la radiación con la cantidad de energía que va a generar un módulo solar fotovoltaico en las condiciones de radiación dadas para el lugar.

Para ello partimos de la energía total diaria recibida, obtenida de las tablas mencionadas anteriormente, y dada en kJ/m2 o langleys. Estos valores representan las medias diarias, calculadas por meses, de energía total recibida durante el día promedio.

Los fabricantes de módulos solares expresan sus valores eléctricos referidos a una radiación de 100 mW/cm2, o lo que es lo mismo, 1000 W/m2. Bastará entonces establecer un nexo de unión entre la energía solar recibida y la cantidad de energía proporcionada por el módulo fotovoltaico a una radiación de 100 mW/cm2; a este valor se le da el nombre de horas de sol pico u horas de sol equivalente, y todo ocurre como si pudiéramos poner el Sol frente al panel solar durante estas horas y retirado después.

La cantidad de energía en este supuesto sería la misma que lo que sucede en realidad, o sea que el Sol describe un arco frente al módulo, generando una energía progresivamente más alta hasta el mediodía solar, y decreciendo posteriormente hasta desaparecer.

Veamos paso a paso el proceso:

1) 1 langley = 1 cal/cm2
2) 1 cal=4.186W.s
3) 1 h = 3600 s
4) 4.186 W.s x (1 h)/(3600 s) = 0.00116 Wh
5) 1 Wh = 1000 mWh
6) Para convertir 1000 m Wh en 100 m Wh: (1000 mWh)/(100 mWh) = 10
7) Luego: 0.00116 Wh x 10 x (100 mWh)/(1 Wh) = 0.0116 x 100 mWh
8) Por tanto:
1 cal/cm2 = 0.0116 x (100 mWh)/cm2
o lo que es lo mismo:
1 langley/día = 0.0116 x (100 mWh)/(cm2.día)

El valor (100 mWh)/cm2 es lo que se ha dado en llamar hora de sol pico (h.s.p.). De esta forma, multiplicando los langleys por el factor 0.0116, obtendremos el número de h.s.p. equivalentes, para poder trabajar más fácilmente en los cálculos de instalaciones.

Según lo anterior, se puede establecer que:

langley x 0.0116 = h.s.p. (kJ/m2) x 0.024 x 0.0116 = h.s.p.

Fuente: Guía técnica de aplicación para instalaciones de energías renovables del Gobierno de Canarias