Al examinar una regla de acero se pueden ver las series de líneas igualmente espaciadas a lo largo de cada borde. Estas líneas se denominan graduaciones y determinan la escala de la regla. La escala de una regla es la relación entre el número de graduaciones y la unidad de longitud, usualmente l pulg ó 1 mm. Es decir, cada serie de líneas o graduaciones en cada borde de la
regla es una escala.
La mayoría de las reglas usadas en el taller tienen escalas donde las pulgadas están divididas en partes fraccionarias. Otras escalas usadas en las reglas incluyen pulgadas en decimales y escalas milimétricas.
Prácticamente cualquier combinación de estas escalas puede conseguirse.
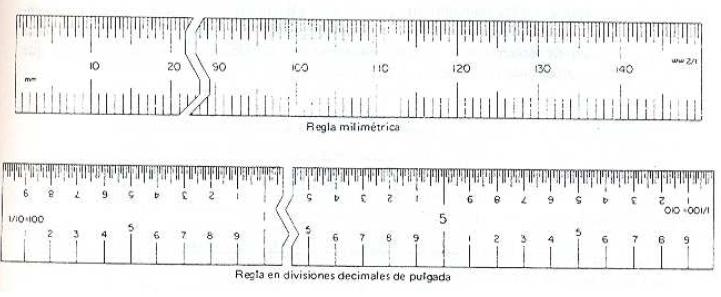
Al leer una regla, identifíquese primero la escala. Muchas de las reglas tienen un número al principio de la escala que indica el número de divisiones por pulgada. Este número también indica la discriminación de la escala.
La discriminación se refiere a la más fina de las divisiones que pueden leerse confiablemente en una herramienta de medición.
En algunas reglas pueden notarse unas series de números más arriba de las marcas de graduación. Estos números se denominan referencias de lectura rápida y ayudan a leer la regla con rapidez y exactitud.
Otro método que se utiliza comúnmente para ayudar a definir la graduación es el escalonamiento de las líneas de graduación. Puesto que las longitudes de dichas líneas varían, puede determinarse más rápidamente una medición exacta que si hubiese que contar cada línea.
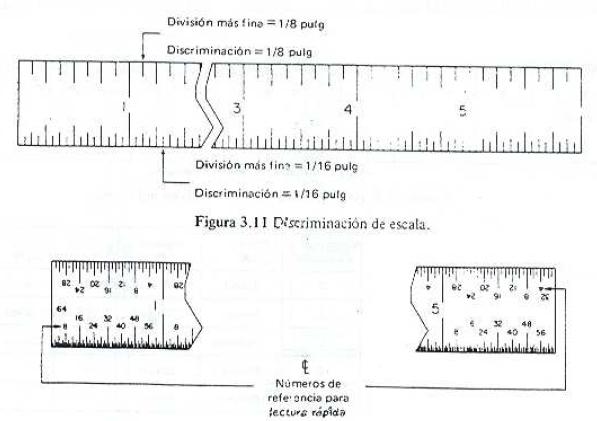
Las reglas fraccionarias dividen cada unidad en 8, 16, 32 ó 64 partes iguales. Estas escalas se leen siempre como partes fraccionarias de una pulgada. Por ejemplo, cada línea en la escala 8 corresponde a 7 pulgada, en la 16 a 17 pulgadas y así sucesivamente.
En la práctica, una regla se lee contando el número de graduaciones entre el punto de referencia y el punto medido. Esta lectura será el número de arriba o numerador de una fracción. El número de la escala hace las veces de denominador ó número de abajo de la fracción.
Por ejemplo, si se leen 3 líneas en la escala 8, la lectura es + pulg. De igual modo, si se leen 5 líneas en la escala 16 el valor medido será 1. En los casos en que la lectura es una fracción reducible, tal como 12 líneas en la escala 16, o sea 12/16 pulgadas, habrá que reducir la fracción a su mínima expresión: pulg X : = 1
Se puede notar que en las escalas 3 y 6 los números de referencia para lectura rápida están arriba de cada graduación de 7 pulg. Estos números se utilizan como marcadores para indicar d número de divisiones en cada división de 9 pulg. Como la escala tiene el doble de graduaciones que la escala 32, los números de referencia en la escala t,-+ son el doble de los correspondientes a la escala 32.
Para lectura rápida, de manera que se suma 28 + 1 = 29. Puesto que la escala utilizada es 32, la lectura es en pulg. Otro punto que es necesario recordar cuando se lee una regla es sumar las unidades de pulgadas, como se muestra en la figura 3.16. Esta lectura es 1 t pulg y no sólo pulg.
Leer una escala en pulgadas decimales también es sencillo. De nuevo, el primer paso será identificar la escala. Las escalas en pulgadas decimales por lo general están graduadas en décimas, cincuentavas y centésimas de pulgada. Algunas veces, este estilo de graduación se prefiere al de escalas fraccionarias. Como las lecturas pueden transferirse a unidades decimales directamente, no hace falta referirse a una tabla de equivalentes decimales.
Cuando se use una regla en pulgadas decimales, observe la posición del punto medido y cuente el número de graduaciones des de el marcador de referencia al punto medido.
Los números de referencia utilizados en esta escala indican el número de divisiones en grupos de 10. Por consiguiente el número 1 es igual a 10. el 2 es igual a 20, el 3 a 30 y así sucesivamente para cada pulgada. Para convertir esta lectura a su valor decimal basta con multiplicar tanto el numerador como el denominador por 10.
Fuente: Apuntes de Metrología de la UNIDEG
