La regla de tres es la operación aritmética que consiste en determinar un término de una proporción cuando se conocen tres.
Cuando tengamos un problema en el que debemos aplicar la regla de tres para solucionarlo, es necesario indagar primero si las cantidades involucradas son directamente proporcionales o son inversamente proporcionales, ya que si no investigas que tipo de proporcionalidad tienen la variables puedes aplicar un procedimiento erróneo para la resolución del problema.
Ejemplo:
Problema 1
Para resolver este problema se aplica la regla de tres para proporcionalidad directa.
Un grifo vierte 160 litros de agua en 4 minutos, ¿cuántos litros verterá en 6 minutos?
Los datos de este problema pueden interpretarse de la siguiente manera: 160 litros son a 4 minutos, entonces ¿cuántos litros serán a 6 minut os?.
En el caso del problema, las cantidades involucradas son: litros de agua y tiempo.
Si aumenta el tiempo aumenta la cantidad de agua vertida por el grifo y si disminuye el tiempo disminuirá la cantidad de agua, así que las cantidades son directamente proporcionales.
Para resolver este tipo de problemas se colocan las variable involucradas de la siguiente manera (litros en una columna y tiempo en otra).
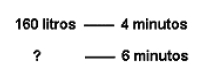
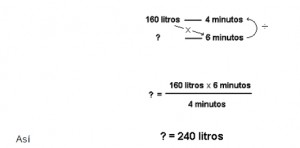
Esto se lee “160 litros son a 4 minutos entonces, ¿cuántos litros serán a 6 minutos?”
SOLUCIÓN : Para encontrar el valor de la incógnita multiplicamos los elementos de la diagonal donde no se encuentra la incógnita y el resultado lo dividimos por el elemento sobrante, esto es

el agua vertida por el grifo en seis minutos será d oscientos cuarenta litros.
Problema 2. Cuatro albañiles hacen una barda en 10 horas, ¿en cuánto tiempo harán esa barda 6 albañiles?.
En este caso las cantidades involucradas son: númer o de albañiles y tiempo, pero a diferencia del problema 1 al aumentar una de las cantidades disminuye la otra.
Si aumenta el número de albañiles disminuirá el tiempo necesario para la construcción de la barda, y si disminuye el número de albañiles aumentará el tiempo de construcción, así que las cantidades son inversamente proporcionales.
Para resolver este tipo de problemas se colocan las variable involucradas de manera como lo hicimos en el problema 1, por columnas sin mezclar variables (albañiles en una columna y tiempo en otra), pero en este caso de proporcionalidad inversa la incógnita la encontraremos con un procedimiento ligeramente diferente.

SOLUCIÓN: Cuando la proporcionalidad es inversa se multiplican las cantidades de la fila donde no está la incógnita y el resultado se divide entre la cantidad restante (esto es la regla de tres para proporcionalidad inversa).
el tiempo requerido para que seis albañiles construyan la barda será de 6.66 horas.
Fuente: Apunte de matemáticas básicas de la UNIDEG.
