Representación geométrica de las desigualdades

Representación geométrica de las desigualdades

3X1 + 5 X2 < = 15
500X1+200X2 <= 1000

Si por el momento se considera a estas desigualdades como igualdades, se tiene

3X1 + 5 X2 = 15
500X1+200X2 = 1000

o lo que es lo mismo

X2 = 3 – (3/5)X1
X2 Cerv.Obscura

Img21_1
X2 = 5 – (5/2)X1

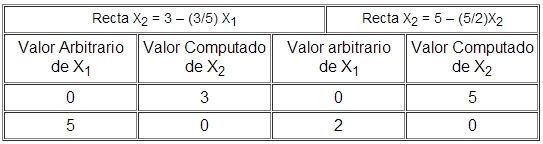
Si arbitrariamente se le da valores a X1 se obtiene el correspondiente valor de X2 en ambas rectas. Un par de valores arbitrarios de X1 generarían 2 puntos, que unidos dan la recta en cuestión.

Se dan a X1 el valor cero en ambas rectas, y los valores cinco y dos a X2 respectivamente. La tabla a continuación da el valor de X2:

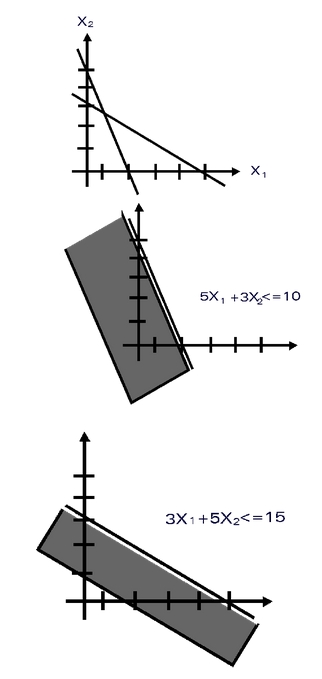
Cualquier punto (X1,X2) satisface la restricción 5X1+2X2 < = 10 en las zonas sombreadas, mientras que en la zona blanca de la misma figura viola la restricción.

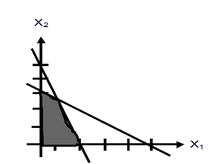
Los puntos (X1,X2) contenidos dentro del área sombreada, son los únicos que satisfacen las restricciones laborales, de capital y de no – negatividad, simultáneamente. El industrial tiene que buscar dentro de esa infinidad de puntos, cuáles son los que producen la mejor utilidad Z. Por ejemplo un punto A, donde X1=0 y X2=0, satisface todas las restricciones y no – negatividad como se muestra a continuación:

3(0) + 5(0) = 0 <= 15

500(0)+200(0) = 0 <= 1000

pero produce una utilidad de Z = 5000(0) +3000(0) = 0.

El punto B donde se producirían X1 = 1000 litros de cerveza clara y X2= 1000 litros de cerveza obscura, también satisface todas las restricciones

3(1) + 5(1) = 8 <= 15

500(1)+200(1) = 700 = 0, 1>=0

y produce una utilidad de Z = 5000(1) +3000(1) = 8000 pesos, que es una utilidad mucho mejor que la obtenida en el punto A. El punto C donde se producirían X1=3000 litros de cerveza clara y X2=3000 litros de cerveza obscura generarían una utilidad de Z = 5000(3) +3000(3) = 24000 pesos.

Que es una utilidad mucho mejor que la producida por los puntos A y B. Sin embargo, la producción del punto C viola las restricciones de personal y de capital. La primera porque utiliza 24 personas, cuando el máximo permisible son 15,

3(3) +5(3) = 24 no es menor o igual que 15, mientras que la segunda, porque se están utilizando 2100 pesos, cuando el máximo permisible son 1000, 500(3) +200(3) = 2100 no es menor o igual que 1000.

Esta región sombreada lleva el nombre de región de factibilidad.

A continuación se verá cómo puede obtenerse gráficamente el punto (X1,X2) que da el nivel de la producción, que satisfaciendo ambas restricciones proporciona la utilidad óptima.

La función de utilidad se expresa como

Z = 5000 X1 +3000 X2

Supóngase que Z es igual a 15000. Esto implica

15000 = 5000 X1 +3000 X2 o sea

X2 = 5 – (5/3) X1.

Dándole a X1 valores arbitrarios de 0 y 3, se obtiene respectivamente valores de X2 iguales a 5 y 0. Al unir los puntos (0,5) y (3,0) con una recta, se obtendrá el lugar geométrico de todos los puntos (X1,X2) que satisfacen la recta.

Gráficamente se obtiene:

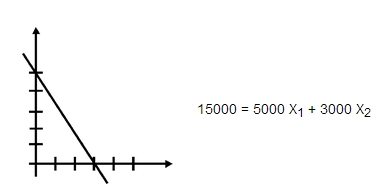
Haciendo Z ahora igual a 10000, se obtiene una recta paralela a la anterior pero desplazada un poco hacia abajo. De la misma manera con una Z = 30000 se obtendría otra recta paralela a las dos anteriores, pero desplazada un poco hacia arriba.

Gráficamente se tiene:

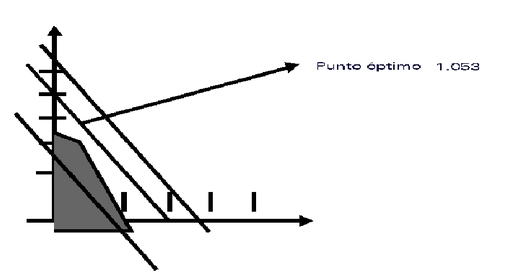
A estas alturas se puede afirmar que si se desplaza la recta hacia abajo, el valor de Z disminuye, mientras que un desplazamiento hacia arriba aumentaría el valor de Z.

LA pregunta del usuario que debe responder se cuál es el máximo desplazamiento hacia arriba, que proporciona el mayor valor Z, y cuya correspondiente producción no viole las restricciones de personal y capital.

Un momento de reflexión observando la figura se convencerá que el punto 0 de coordenadas (X1*,X2*) , es el punto buscado.

En este ejemplo, ese punto es el siguiente:

X1* = 1053 litros de cerveza clara
X2* = 2368 litros de cerveza obscura,

Que generan una utilidad óptima de

Z* = 5000(1.053) +3000(2.368) = 12369 pesos.

Fuente: Apunte de Investigación de Operaciones del Instituto Tecnológico de la Paz