Dos líneas rectas perpendiculares entre sí, que se cortan, constituyen un sistema de ejes coordenados rectangulares.
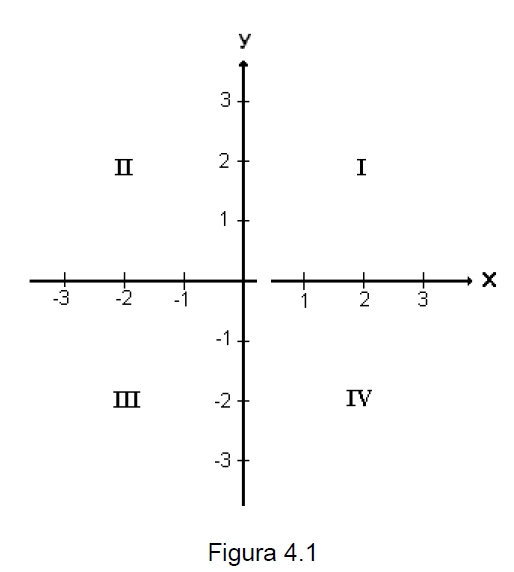
La recta horizontal de la figura 4.1 se llama eje x o eje de las abscisas, la recta vertical se llama eje y o eje de las ordenadas. El punto donde se cruzan los ejes se llama origen de coordenadas.
El sistema de coordenadas rectangulares también es llamado sistema de coordenadas cartesianas en honor al célebre matemático francés Rene Descartes, fundador de la geometría analítica.
Los ejes dividen al plano en cuatro partes llamadas cuadrantes, los números romanos de la figura anterior indican cuales son el primero (I), segundo (II), tercero (III) y cuarto cuadrante (IV).
Cada punto del plano está determinado por un par de números llamados coordenadas del punto en cuestión.
Ejemplo:
La figura 4.2a muestra cuatro puntos (en los diferentes cuadrantes) denotados con P1, P2 , P3 y P4 . En la figura 4.2b observarás que cada uno de los puntos anteriores se “conecta” a los ejes mediante líneas punteadas perpendiculares a los mismos, esas líneas nos llevan hasta la abscisa (o coordenada x) y la ordenada (o coordenada y) de cada punto.
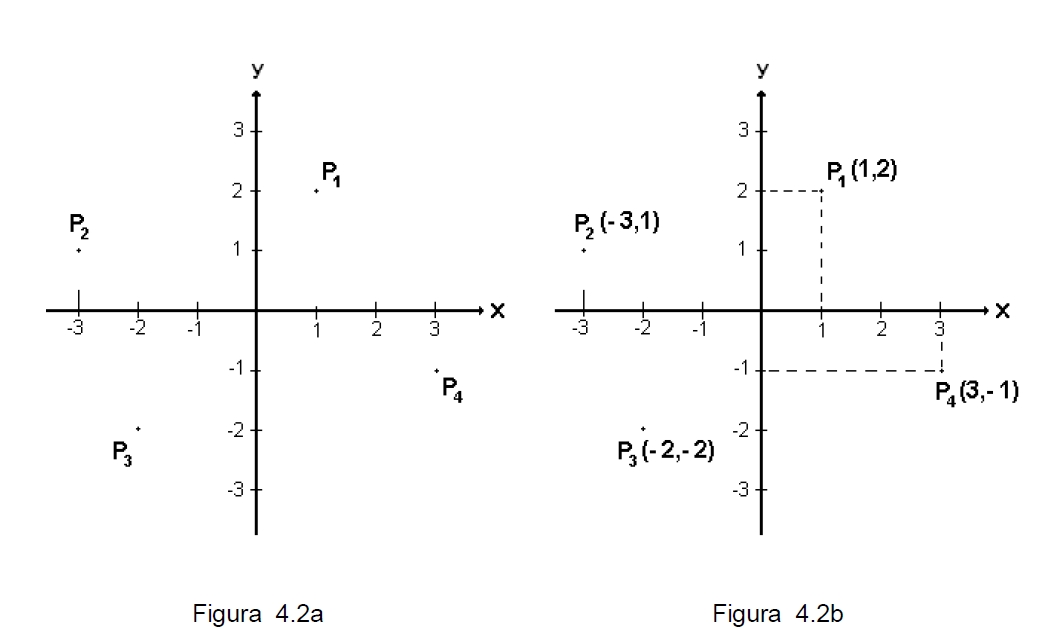
Así, el punto P1 tiene por coordenadas al par ordenado (1,2), el punto P2 tiene por coordenadas al par ordenado (-3,1), las coordenadas de P3 son (-2,-2) y las coordenadas de P4 son (3,-1).
En general, todo punto del plano tendrá coordenadas (x,y) y los signos de x y y dependerán del cuadrante en que se encuentre el pun to. A la pareja de números (x,y) se le llama par ordenado ya que x y yno pueden intercambiar posiciones (siguen un orden), porque si así lo hicieran representarían dos puntos diferentes.
Ejemplo:
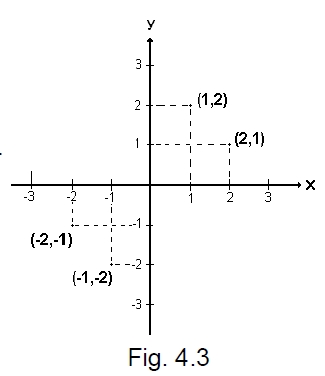
El punto (1,2) no es el mismo que el punto (2,1) como se muestra en la figura 4.3, de la misma manera el punto (-2,-1) no es el mismo que el punto (-1,-2). También los signos de las coordenadas son importantes, (2,1≠) (-2,-1).
Distancia entre dos puntos
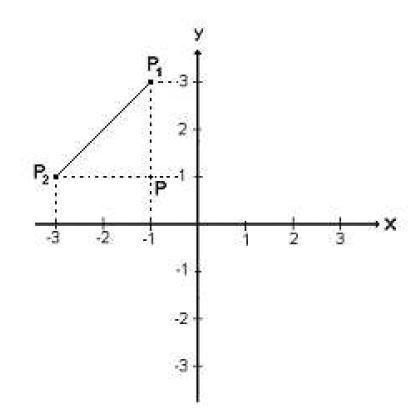
Ela siguiente figura. Se quiere calcular la distancia entre los puntos P1 y P2 . Como podrás ver, los puntos P1 , P2 y P forman un triángulo rectángulo cuyos lados son:
La línea continua entre P1 y P2 , la línea a trazos entre P1 y P , y la línea a trazos entre P y P2.
La distancia entre los puntos P1 y P2 es la longitud de la hipotenusa del triángulo P1 P2 P. La longitud de la línea a trazos entre P1 y P se calcula tomando la diferencia de las ordenadas de los puntos P1 y P, mientras que la longitud de la línea a trazos entre P y P2 se calcula tomando la diferencia de las abscisas de los puntos P y P2.
Esto es, distancia P1 P = 3 –1 =2 , distancia P P2 = -1 – (-3) =2
Por lo tanto, aplicando el teorema de Pitágoras, la distancia P1 P2 está dada por:
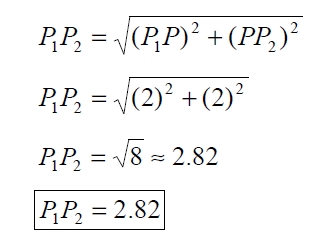
En general, la distancia “ d ” entre dos puntos del plano P( x2 , y2 ) y P1( x1 , y1 ) está dada por
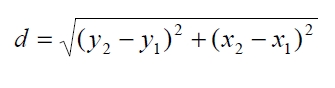
Fuente: Apunte de matemáticas básicas de la UNIDEG.
