Valor futuro y valor presente de las anualidades simples ciertas y ordinarias inmediatas
Este tipo de anualidades es el más frecuente y, por esto, cuando se dice simplemente anualidad, se supone que se trata de una anualidad simple cierta ordinaria. La tasa de interés es, por lo general, una tasa de interés nominal anual.
En caso de que la tasa no sea nominal, se aclarará diciendo tasa efectiva anual. Si la tasa dada es nominal, sin especificación de período de capitalización, la tasa efectiva en el período de pago es el cociente entre la tasa nominal y el número anual de pagos.
Símbolos que se utilizan en las anualidades.
R = pago periódico de una anualidad o renta. i = tasa efectiva por período de capitalización. j = tasa nominal anual.
m = número de capitalizaciones en el año.
j(m) = tasa nominal con m períodos de capitalizaciones en el año. n = número de períodos de pago.
S = monto de una anualidad.
A = valor actual o presente de una anualidad.
Cálculo del monto. Los pagos R efectuados al final de cada período ganan interés compuesto, hasta la fecha final.
Estableciendo la ecuación de equivalencia para la fecha final como fecha focal, tendremos:
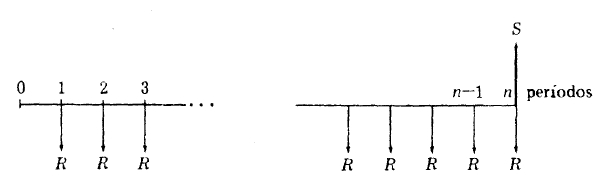
Cada pago efectuado al final de período capitaliza los intereses en cada uno de los períodos que le siguen.
El primer pago acumula durante (n — 1) períodos, el segundo (n — 2) períodos y, asi:,sucesivamente hasta el último pago que no gana intereses, ya que su , pago coincide con la fecha de término.
Los montos respectivos de los pagos R comenzando por el último serán:
El monto total S de la anualidad es igual a la suma de los montos producidos por las distintas rentas R, o sea:
Los términos del segundo miembro forman una progresión geométrica de n términos, razón (1 + i) y primer término R. Aplicando la fórmula de la suma dada en 0.11, se tiene:
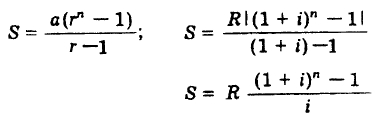
Si el valor de cada pago R es de una unidad monetaria, el monto S corresponderá al monto de una anualidad de uno por período y se expresa con el símbolo Sn┐i; que se lee s sub n al i; sustituyendo este símbolo en la fórmula, se obtiene:
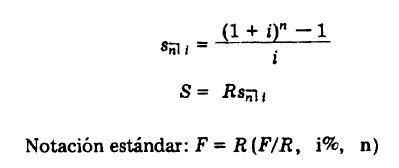
Los valores de Sn┐ i pueden calcularse con calculadoras actualmente, disponemos de máquinas de calcular que se construyen cada día más completas, manuales y compactas y a precios cada vez más económicos; las calculadoras electrónicas forman par-te hoy del equipo de trabajo de un estudiante.
Disponiendo de una calculadora común que tenga una memoria y las funciones logaritmo y exponencial, el estudiante podrá trabajar directamente las operaciones que exigen los problemas.
En la práctica, son numerosos los cálculos financieros que se efectúan utilizando tablas; por esta razón es necesario que el estudiante se ejercite en el uso de ellas; los valores de Sn┐i , calculados para las tasas y números de períodos que utilizan en los problemas se expresan i en tanto por ciento y escriben, por ejemplo, S20┐3% , para expresar el montó de 1 en 20 períodos al 3% efectivo en el período. Nosotros utilizaremos la expresión decimal y escribiremos S20┐0.03.
Fuente: Apunte de Matemáticas financieras de la UNIDEG
