Álgebra de las proposiciones o álgebra de Boole

Las tres operaciones que hemos indicado para las proposiciones o sentencias, es decir  la negación (no), la conjunción (y) y la disyunción (O), se demuestra que verifican los axiomas del llamado álgebra de Boole dado que el álgebra de las proposiciones está dotada de las mismas propiedades características que un álgebra de conjuntos, con la adecuada correspondencia ente operaciones.

Sin embargo, lo que interesa aquí es indicar que el álgebra de Boole sirve como modelo matemático adecuado de representación de los acoplamientos de circuitos eléctricos equipados con  conmutadores. Su importancia u para nosotros radica en el hecho de que además de emplearse en las redes de distribución de la energía eléctrica, en las centrales de comunicación telefónica, etc., se emplea en los ordenadores.

Para iniciar nuestro estudio de dichos circuitos cabe indicar que los conmutadores (y esta denominación incluye también  todos los dispositivos eléctricos y electrónicos tales como válvulas, transistores, etc.) sólo pueden encontrarse en dos estados posibles: o están abiertos o están cerrados. En el primer caso, el interruptor abierto impide el paso de la corriente a través del circuito, mientras que el segundo, es decir, cuando el conmutador está cerrado, la corriente pasa libremente a través suyo.

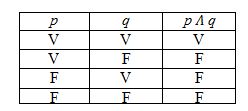
«La tabla de verdad correspondiente a la disyunción (representada mediante W) y que corresponde a la proposición o p o q o ambos, revela que sólo en el caso en que ambas sean falsas la proposición resultante lo es también»

El circuito eléctrico más simple a este respecto es el formado por una fuente de corriente (una pila o un generador cualquiera), un hilo conectado a sus bornes y un conmutador y una bombilla intercalados en él. Con este tipo de conexión pueden darse dos situaciones diferentes: o bien el conmutador está cerrado, y por lo tanto la corriente fluye a través del circuito y la bombilla se enciende, o bien el conmutador esta abierto, con lo que impide el paso de la corriente por el circuito y la bombilla no luce.

El siguiente nivel de complicación proviene del hecho de conectar en un mismo circuito más de un conmutador siendo los casos más sencillos las llamadas conexiones en serie y en paralelo. En la primera se intercalan dos conmutadores, uno tras otro, en el hilo que une los bornes de la fuente y la bombilla. En esta  situación, las posiciones posibles de ambos conmutadores que determinarán si la bombilla luce o no, es decir, si pasa o no pasa la corriente, son cuatro.

Si ambos conmutadores están cerrados, la corriente pasa; Si ambos están abiertos, no pasa; mientras que si uno de ellos está cerrado y el otro abierto, tampoco pasa corriente, es decir, la bombilla no luce. La conexión en paralelo de los dos conmutadores muestra un aspecto distinto. En este caso los dos se intercalan en el hilo pero constituyendo caminos diferentes para el paso de la corriente.

De este modo cuando ambos conmutadores están cerrados la corriente pasa, cuando lo está uno y el otro no, la corriente sigue pasando y sólo en el caso de que ambos estén cerrados la corriente no puede pasar.

De todo lo dicho hasta ahora se deduce que la forma más elemental de representar estas dos situaciones es mediante las operaciones suma y producto (que serán equivalentes a la conjunción y disyunción antes mencionadas),

En el caso de la negación, la situación representa una dependencia entre los dos conmutadores ya que cuando uno está abierto, el otro está cerrado y viceversa, como vemos, hay una analogía clara con el álgebra de proposiciones, por lo que se demuestra que la de Boole es un modelo matemático adecuado del álgebra de los circuitos lógicos.

En el caso de los ordenadores, su empleo ha llevado a crear unos símbolos adecuados, compuestos por una “Caja negra” (es decir, un elemento del cual conocemos la salida para una cierta entrada pero del que ignoramos el modo en que dicha salida se genera) sobre la que se indica la operación y en cuyo extremo izquierdo se señalan las entradas (generalmente mediante las letras A, B, C, etc.) y en el derecho las salidas (S).

Para la aplicación a los ordenadores de estos circuitos lógicos se suele operar con los símbolos 1 y 0 o (ó L y 0), hablándose, en y dicho caso, de tres operaciones que son la suma lógica, el producto lógico y la complementación, representadas mediante los símbolos  respectivamente.