Coeficiente de producción

Una de las preocupaciones de los empresarios es buscar la máxima ganancia; como se anotó anteriormente una forma de encontrarla es reduciendo costos. Para lograrlo es importante hacer la función de producción, que es una fórmula que representa los coeficientes de factor para producir una unidad; el problema que se enfrenta ahora es explicar qué es un coeficiente de producción, quizá con un pequeño ejemplo se pueda captar la idea.

Supongamos que Marite quiere producir camisas para hombre de determinada talla y cierto estilo, la pregunta que se tiene que resolver es ¿qué se necesita para producir camisas? Así, encontramos que requerimos tela, botones, hilo, bies, mano de obra, maquinaria, espacio de planta, etcétera.

Si llamamos X a una unidad de producción sería el resultado de la combinación de los factores antes citados; y no se nos ocurriría combinar los factores sin antes cuantificar la necesidad de cada uno de ellos; así llamaremos “a” a la tela, “b” a los botones, “c” al hilo, “d” al bies, “e” a la mano de obra, “f” a la maquinaria, “g” al espacio de la planta.

Con las letras minúsculas se representa los coeficientes del factor; ahora es preciso que tomemos en cuenta que el coeficiente del factor productivo es la cantidad mínima necesaria que se requiere de él para producir una unidad.

X= (a, b, c, d, e, f, g, etc.)

Ésta es la fórmula que representa la función de producción; si los coeficientes a los que se refiere la fórmula los sustituimos por su costo se estaría en condiciones de determinar el costo de la unidad de producción.

Pero antes de tomar alguna decisión, se debe saber que la mayor de las veces el rendimiento de los factores productivos no es constante porque obedece a la ley de la proporción de los factores y costos que Marite debe cuantificar.

Así mismo, hay productos en que el rendimiento de los factores productivos es proporcional y son sustituibles sin que se afecte el monto de producción. Siguiendo con el ejemplo de Marite en la producción de camisas, ella tiene la función de producción Q = f (K, L) y en el supuesto de que Q = 80 tendríamos que 80 = f (K, L.).

Como los factores capital (K) y mano de obra (L) son sustituibles sin afectar la cantidad de producción, se puede cambiar L por K y viceversa, según convenga a quien decide si atendiera a costos o cualquier otro interés.

El cuadro presenta combinaciones de mano de obra (L) y capital (K)

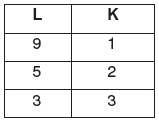
Representación gráfica de la línea de isocuantas o curva de producto constante o isoproducto o curva de nivel de producción.

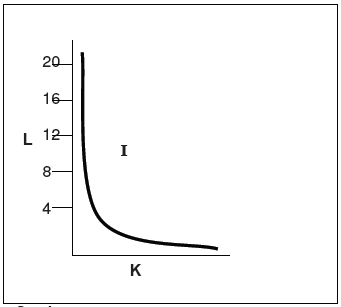
La línea I representa la producción Q=80; es importante aclarar que esa cantidad se alcanza en cualquier punto de la línea, con la combinación que
arroje la mano de obra y el capital.

Por ello, esa línea para Marite le dará la misma satisfacción, puesto que ésta persigue una producción igual a 80; así pues, la línea es llamada de indiferencia y cuando se refiere a la misma producción es de isocuanta, por lo que también es llamada línea de producto constante.

Fuente: Apunte de Microeconomía de la FCA, UNAM.