Comparación entre simple e interés compuesto

Por ser objetiva, la mejor forma de comparar los montos es dibujando las gráficas correspondientes a una misma tasa, para el interés simple y el compuesto.

Sea por ejemplo la tasa del 20% y un capital de $1000. Los montos son S = 1000 [1 + n(0,20)] para el interés simple y S = (1 + 0,20)n para el interés compuesto.

Función discreta

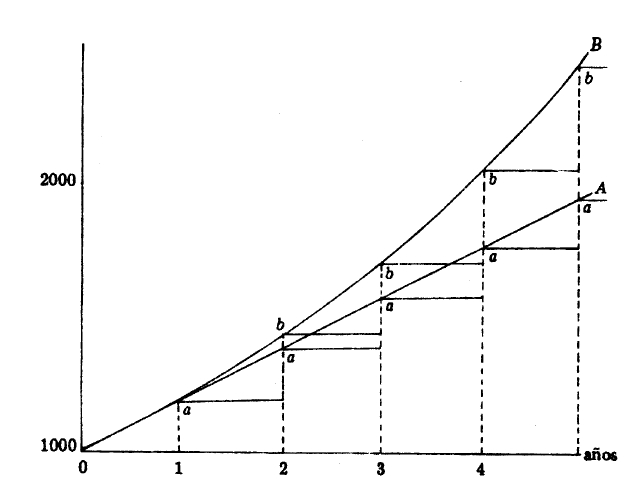
a = monto de $1000 al interés simple del 20%
b = monto de $1000 al interés compuesto del 20%

Función continúa

A línea recta S =1000 + n (1,20)
B función exponencial S = 1000(1,2)n

El monto a interés compuesto crece en razón geométrica y su gráfica corresponde a la de una función exponencial. Por su parte, el monto a interés simple crece en progresión aritmética y su gráfica es una línea recta.

Fuente: Apunte de Matemáticas financieras de la UNIDEG