La representación de datos comprimidos ha ido adquiriendo cada vez más importancia debido a la utilización de mayores cantidades de información, sobre todo en las aplicaciones multimedia. Comprimiendo datos se optimiza tanto la memoria utilizada para su almacenamiento como el tiempo de transmisión por las redes.
Uno de los métodos de compresión más conocido es el llamado de Lempel-Ziv (LZ), que aprovecha de forma bastante simple las repeticiones de ciertos patrones de bits que aparecen en una cadena. Se aplica a cualquier tipo de información representada por una cadena de bits y se realiza en los siguientes pasos:
1) Se descompone la cadena de modo que no se repita el mismo patrón de bits. Para ello:
a) se coloca un separador después del primer dígito
b) el siguiente separador se coloca de modo que el fragmento entre separadores sea el más corto posible que no haya aparecido previamente.
El proceso continúa hasta fragmentar toda la cadena.
Ejemplo: la cadena de bits
101100101001101001000
se fragmentaría de la forma siguiente:
1-0-11-00-10-100-110-1001-000
2) Se enumeran los fragmentos.
![]()
Cada fragmento es siempre la concatenación de un fragmento prefijo aparecido con anterioridad, y de un bit adicional, 0 ó 1. Por ejemplo, el fragmento número 3, 11, es el número 1 seguido de un 1; el número 6, 100, es el 5 seguido de un 0; y así sucesivamente.
3) Se sustituye cada fragmento por el par (número de prefijo, bit adicional). El 0 indicará el prefijo vacío. En nuestro ejemplo:
(0,1)-(0,0)-(1,1)-(2,0)-(1,0)-(5,0)-(3,0)-(6,1)-(4,0)
4) Se codifican en binario los números de los prefijos.
En nuestro ejemplo, como aparecen siete prefijos, se necesitan tres bits para codificarlos:
(000,1)-(000,0)-(001,1)-(010,0)-(001,0)-(101,0)-(011,0)-(110,1)-(100,0)
5) Se quitan los paréntesis y los separadores y obtenemos la cadena de bits comprimida:
000100000011010000101010011011011000
La descompresión se realiza siguiendo el proceso inverso y conociendo el número de bits de la codificación del prefijo, tres en nuestro ejemplo. Sabemos entonces que cada fragmento está codificado por cuatro bits, tres para el prefijo y uno para el bit adicional:
000100000011010000101010011011011000
1) 0001-0000-0011-0100-0010-1010-0110-1101-1000
2) (000,1)-(000,0)-(001,1)-(010,0)-(001,0)-(101,0)-(011,0)-(110,1)-(100,0)
3) (0,1)-(0,0)-(1,1)-(2,0)-(1,0)-(5,0)-(3,0)-(6,1)-(4,0)
1 2 3 4 …….
4) 1-0-11-00 …….
En el ejemplo anterior la cadena resultante es más larga que la original, en contra del propósito del método. La causa es la poca eficiencia del método para cadenas muy cortas. Cuando se aplica a una cadena muy larga, los fragmentos crecen en longitud más rápidamente que las subcadenas de bits necesarias para su codificación.
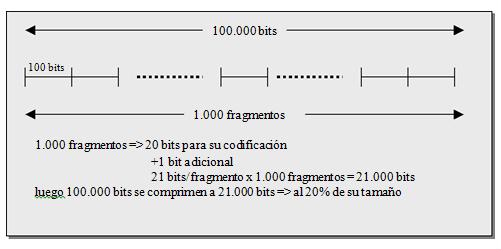
Por ejemplo, supongamos que una cadena de 100.000 bits se ha dividido en 1.000 fragmentos con un tamaño medio de 100 bits (los primeros serán probablemente más cortos y los últimos más largos). Para codificar el prefijo solo se necesitan 10 bits (210 = 1024). Por tanto cada fragmento estará codificado por 11 bits (los 10 del prefijo más el bit adicional), mientras que su longitud original era de 100 bits. Es decir, el método lograría comprimir el fichero de datos a un 10% de su tamaño original.
Está claro que cuanto más largos sean los fragmentos, más eficaz será el método. Esto ocurre si la cadena tiene muchas repeticiones. El caso extremo es una cadena con todo ceros. En este caso la fragmentación es muy simple:
0-00-000-0000-00000-000000-0000000-…

Una cadena con n ceros se dividiría en un número de fragmentos m -1 tal que:
n = 1+2+3+…+(m-1) = m(m+1)/2 (progresión aritmética)
lo que implica que aproximadamente ![]()
Para 1MB, que son 8.388.608 bits, tendríamos 4.096 fragmentos y necesitaríamos sólo 12 bits para describir el prefijo. Por tanto, necesitaríamos 13 bits para describir cada fragmento o 53.248 bits para describir el fichero entero. El fichero habría quedado reducido a 6,65 KB, es decir, al 0,63 % de su tamaño original.
El caso opuesto es una cadena de bits cuya fragmentación contenga todas las subcadenas posibles. Por ejemplo, hay 128 subcadenas de 8 bits. Si la fragmentación resultara en una concatenación de todas ellas, se necesitarían 8 bits para describir el prefijo y 9 para describir el fragmento, mientras que la longitud original de los fragmentos es de 8 bits. El método resultaría perfectamente inútil en este caso.
El método LZ es más eficaz cuanto más regular sea la cadena, es decir, cuantas más repeticiones contenga. Esta característica está de acuerdo con el teorema de Shannon, que afirma que cuanto más regular y menos aleatoria sea una cadena (menor sea su entropía), mayor será su grado de compresión. Shannon demostró que para una cadena de n bit aleatorios y completamente independientes unos de otros la entropía vale:
![]()
donde p es la probabilidad de que cada bit sea un 1.
Como el programa WinZip de Windows utilizan alguna variante de este método, se puede comprobar empíricamente la fórmula de Shannon creando ficheros de cadenas de bits aleatorios con diferentes probabilidades p = 0,01; 0,1; 0,2, etc. y comprimiendo los ficheros con WinZip. Después se podrá observar que los tamaños comprimidos están en la misma relación que los previstos en la fórmula de Shannon.

Fuente: Estructura de Computadores, Facultad de Informática, UCM
