En 1951 Savage argumenta que al utilizar los valores Xij para realizar la elección, el quien decide compara el resultado de una alternativa bajo un estado de la naturaleza con todos los demás resultados, independientemente del estado de la naturaleza bajo el que ocurran.
Sin embargo, el estado de la naturaleza no es controlable por el quien decide, por lo que el resultado de una alternativa sólo debería ser comparado con los resultados de las demás alternativas bajo el mismo estado de la naturaleza.
Con este propósito Savage define el concepto de pérdida relativa o pérdida de oportunidad rij asociada a un resultado xij como la diferencia entre el resultado de la mejor alternativa dado que ej es el verdadero estado de la naturaleza y el resultado de la alternativa ai bajo el estado ej:
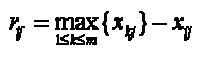
Así, si el verdadero estado en que se presenta la naturaleza es ej y el quien decide elige la alternativa ai que proporciona el máximo resultado xij, entonces no ha dejado de ganar nada, pero si elige otra alternativa cualquiera ar, entonces obtendría como ganancia xrj y dejaría de ganar xij-xrj.
Savage propone seleccionar la alternativa que proporcione la menor de las mayores pérdidas relativas, es decir, si se define ri como la mayor pérdida que puede obtenerse al seleccionar la alternativa ai,
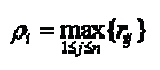
Así de acuerdo con el criterio de Savage la mejor opción resulta ser la siguiente:
![]()
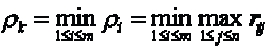
Conviene destacar que, como paso previo a la aplicación de este criterio, se debe calcular la matriz de pérdidas relativas, formada por los elementos rij. Cada columna de esta matriz se obtiene calculando la diferencia entre el valor máximo de esa columna y cada uno de los valores que aparecen en ella.
Partiendo del ejemplo de construcción del aeropuerto, la siguiente tabla muestra la matriz de pérdidas relativas y el mínimo de éstas para cada una de las alternativas.
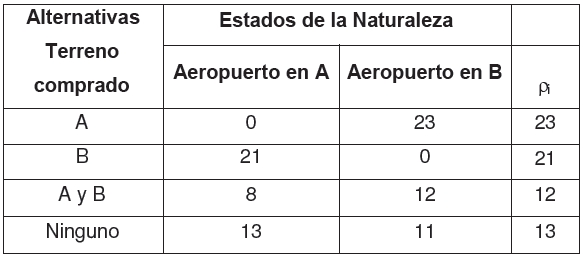
El mayor resultado situado en la columna 1 de la tabla de decisión original es 13; al restar a esta cantidad cada uno de los valores de esa columna se obtienen las pérdidas relativas bajo el estado de la naturaleza Aeropuerto en A.
De la misma forma, el máximo de la columna 2 en la tabla original es 11; restando a esta cantidad cada uno de los valores de esa columna se obtienen los elementos rij correspondientes al estado de la naturaleza Aeropuerto en B.
Como puede observarse, el valor Pi menor se obtiene para la tercera alternativa, por lo que la decisión óptima según el criterio de Savage sería comprar ambos terrenos.
– Crítica
El criterio de Savage puede dar lugar en ocasiones a decisiones poco razonables. Para comprobarlo, consideremos la siguiente tabla de resultados:
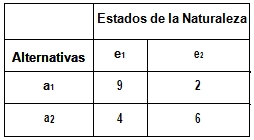
La tabla de pérdidas relativas correspondiente a esta tabla de resultados es la siguiente:
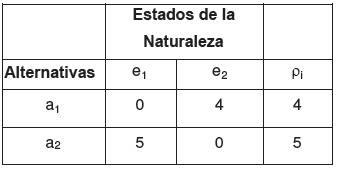
La alternativa óptima es a1. Supongamos ahora que se añade una alternativa, lo que da lugar a la siguiente tabla de resultados:
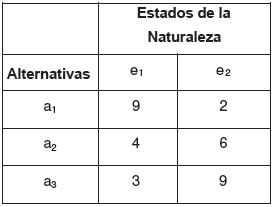
La nueva tabla de pérdidas relativas sería:
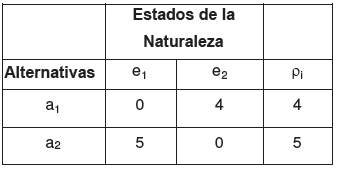
El criterio de Savage selecciona ahora como alternativa óptima a2, cuando antes seleccionó a1. Este cambio de alternativa resulta un poco paradójico: supongamos que a una persona se le da a elegir entre peras y manzanas, y prefiere peras. Si posteriormente se la da a elegir entre peras, manzanas y naranjas, ¡esto equivaldría a decir que ahora prefiere manzanas!.
Fuente: Apunte de Microeconomía de la FCA, UNAM.
