Deducción de la fórmula del monto a interés compuesto
Deducción de la fórmula del monto a interés compuesto Si la cantidad presente es dinero, podemos imponer la condición que en un período de tiempo t crezca con crecimiento natural, por adición de sus intereses i en cada período.
En el instante t = 0; Y = C (capital inicial), sustituyendo en
Sustituyendo la cantidad presente Y por el monto S; el valor de t corresponde al número de períodos, o sea, es igual a n,
Se tiene:
Tasa instantánea Si en j (m)
suponemos que m crece sin límite (m → ∞) entonces, el período de capitalización es un intervalo de tiempo más pequeño que cualquier cantidad arbitrariamente escogida.
En este caso, se dice que la capitalización es continua y que la tasa es una tasa instantánea.
La tasa instantánea acostumbra a designarse con la letra griega delta (δ).
Por definición
, o simplemente 
De acuerdo con lo estudia en tasas equivalentes:
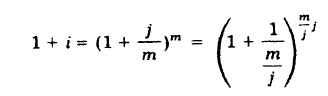
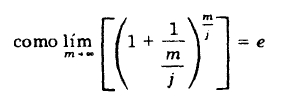
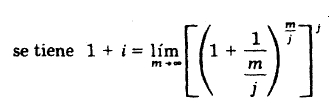
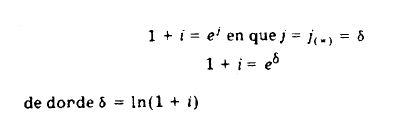
El valor de б se conoce con el nombre de fuerza del interés, y es la tasa continua de crecimiento de una unidad de capital en una operación financiera; en tanto que la tasa efectiva es el interés por unidad de capital en un período.
Fuente: Apunte de Matemáticas financieras de la UNIDEG
