Resuélvase por el método de doble fase el siguiente problema inicial
Sujeto a
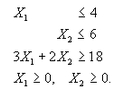
Primero se reescribe el problema como
Sujeto a
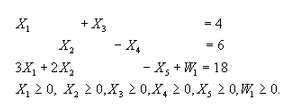
La primera fase consiste en resolver el problema
Sujeto a
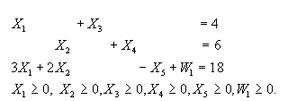
Aplicando el método simplex, una vez que se ha cambiado la función objetivo a 
se tiene
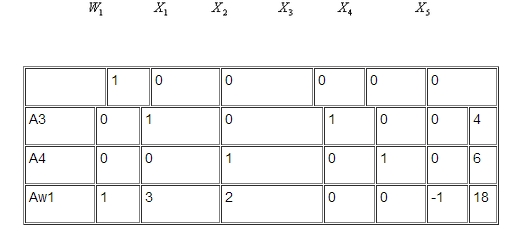Para tener el primer punto extremo se requiere que los vectores de la base sean unitarios. Por lo tanto se convierte
en vector 
Esta es la solución óptima de la fase uno, y como W = 0 el problema original tiene solución. Para empezar la fase dos tómese todo la tabla óptima anterior, únicamente ignorando la columna 
( que ya nos e necesita) y el renglón de los 
Sustitúyase ese renglón por la función objetivo original.
O equivalentemente
Los vectores unitarios e1, e2, e3, que son respectivamente a1, a4, a2, son restaurados por medio de operaciones matriciales elementales.
En este ejemplo no es necesario seguir iterando en la fase dos, pues al restaurar los vectores unitarios correspondientes a la base de la tabla óptima de la fase uno, se obtuvieron por pura coincidencia las condiciones de optimalidad 
para toda j en A.
Por lo general este no será el caso y será necesario hacer varias iteraciones del método simplex en la segunda fase. La solución óptima es la misma que la obtenida en el método gráfico y en el método de penalización, es decir:
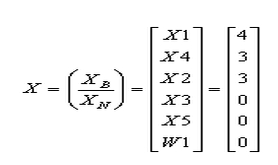
Y h = -Z = -3 o Z = 3.
Fuente: Apunte de Investigación de Operaciones del Instituto Tecnológico de la Paz