MINIMIZAR Z=2X1+X2
Sujeto a:
3X1 + X2³ 3
4X1 +3X2³ 6
X1 +2X2£ 3
X1, X2³ 0
El paso inicial necesita que se conviertan todas las restricciones en desigualdades «£ » y que después se aumenten las variables de holgura. por lo tanto, se obtiene :
MINIMIZAR Z=2X1+X2
Sujeto a:
– 3X1 – X2 + X3 =-3
– 4X1 -3X2 +X4 =-6
X1 +2X2 +X5=3
X1, X2,X3,X4,X5³ 0
Si se intenta expresar este problema como una tabla simplex inicial, se observara que las variables de holgura (X3,X4,X5) no ofrecen una solución inicial factible.
Como este es un problema de minimización y todos los coeficientes de la ecuación objetivo son £ 0, la solución básica inicial. X3=-3,X4=-6,X5=3 es optima pero infactible.
Este problema es del tipo común que se puede manejar a través del método simplex dual.
Tabla óptima inicial pero infactible esta dada como:
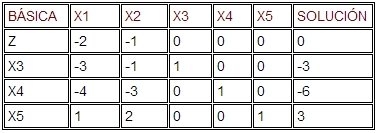
Como el método simples regular, el método de solución esta basado en las condiciones de factibilidad y optimidad. La condición de optimidad garantiza que la solución permanezca siempre optima, mientras que la condición de factibilidad obliga a las soluciones básicas hacia el espacio factible.
Condición de factibilidad
La variable que sale es la variable básica que tiene el valor mas negativo. Si todas las variables básicas son no negativas el proceso termina y se alcanza la solución factible(optima).
Condición de optimidad
La variable que entra se elige de entre las variables no básicas como sigue. Tome los conscientes de los coeficientes del lado izquierdo de la ecuación z entre los coeficientes correspondientes a la ecuación asociada a la variable que sale.
Ignore los cocientes asociados a denominadores positivos o cero. La variable que entra es aquella con el cociente mas pequeño si el problema es de minimización o el valor absoluto mas pequeño de las razones si el problema es de maximización (rompa los empates arbitrariamente).
Si todos los denominadores son cero o positivos el problema no tiene ninguna solución factible.
Después de elegir la variable que entra y la que sale, se aplican las operaciones de renglón como es usual para obtener la siguiente iteración de la solución.
La variable que sale en la tabla anterior es X4 < (=-6) ya que tiene el valor mas negativo. Para la variable que entra, los cocientes son
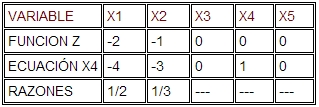
La variable que entra es x2 ya que corresponde al cociente más pequeño 1/3. Aplicando las operaciones renglón como es usual, se encuentra la nueva tabla:
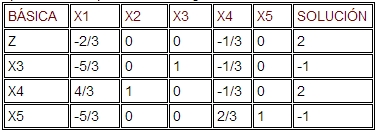
La nueva solución todavía es óptima pero infactible(X3=-1, X5=-1). Si X3 se elige arbitrariamente para que deje la solución, X1 llega a ser la variable de entrada. Esto da :
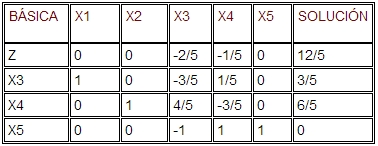
La cual es óptima y factible. La aplicación del método simplex dual es especialmente útil en el análisis de sensibilidad.
Esto ocurre, por ejemplo cuando se agrega una nueva restricción al problema después que se ha obtenido la solución optima. Si esta restricción no se verifica por la solución optima, el problema permanece óptimo pero llega a ser infactible.
Por lo tanto el método simplex dual se utiliza entonces para quitar la infactibilidad en el problema.
Fuente: Apunte de Investigación de Operaciones del Instituto Tecnológico de la Paz
