El otro factor importante para evaluar la incertidumbre requerida es que tan crítica es esa magnitud de interés. Se encuentran en la práctica diferencias en la importancia de las magnitudes que intervienen en un proceso. En los extremos, existen algunas que son vitales para obtener los resultados esperados del proceso, y otras que son sólo de interés superficial, sea por su naturaleza o porque existe un sistema de medición redundante.
Por ejemplo, en la producción de emulsiones medicinales para niños, es vital asegurar la cantidad del agente activo. Evidentemente, incorporarlo en exceso o muy pobremente tendrá consecuencias graves, si no funestas, en las características del producto.
Por otro lado, la cantidad de colorante agregado es importante en términos de la apariencia, pero las consecuencias de no cumplir exactamente con las especificaciones al respecto es ciertamente mucho menos trascendente.
Evaluar qué tan crítica es la medición de una magnitud requiere de criterios objetivos. En la Tabla 1 se muestran, como alternativa, criterios para ello, en términos del riesgo que se corre al no cumplir inadvertidamente las especificaciones. Es necesario insistir que ésta es una alternativa que el usuario puede modificar.
La primera columna de la Tabla l indica la gravedad del riesgo en términos típicos como una guía general Es posible que en algunas organizaciones aparezcan algunos otros criterios.
La segunda columna intenta cuantificar el riesgo en una escala de O a 10, siendo 10 el riesgo más grande. No obstante que sólo se presentan calificaciones pares, es válido asignar cualquier número entre O y 10. Por experiencia, se recomienda determinar la calificación por trabajo en equipo con d fin de integrar las distintas percepciones personales.
La tercera columna muestra el Índice de Riesgo de Medición (IRM), calculado como el resultado de multiplicar el calificador de riesgo por un factor de 2, factor elegido en este caso como típico, pero susceptible de ser cambiado de acuerdo a las políticas de la organización. Por ejemplo, una central nucleoeléctrica preferirá seguramente un factor mayor.

Como se comentó, la incertidumbre de medición requerida para una magnitud depende de la variabilidad y de la importancia de la magnitud en el proceso. La variabilidad está cuantificada por los límites de control y la importancia por el Índice de Riesgo de Medición (IRM).
En concreto, la incertidumbre estándar de medición requerida Ur para una magnitud con límites de control superior e inferior LSC y LIC respectivamente, a la que se ha asignado un IRM es Ur = LSC- LIC / 6 IRM
El divisor «6» supone que los límites de control están calculados a 3 segundos, esto es, que hay 6 desviaciones estándar entre los límites. En otros casos, debe ajustarse ese divisor correspondientemente.
Conviene hacer hincapié en que Ur es la incertidumbre requerida estándar de la medición, esto es, representa una desviación estándar de la distribución resultante de la medición (conviene revisar las modalidades de expresión de la incertidumbre de medición. Ello implica que se requiere que en el 99,7% de los casos aproximadamente, el valor verdadero de la magnitud medida esté en un intervalo de ancho 6 Ur centrado en el valor más probablemente verdadero.
En la Tabla 2 se ilustra la relación entre el IRM y el poder de discriminación del sistema de medición. Cuando IRM=2, el sistema distingue solamente dos categorías: el bueno y el malo. Conforme IRM aumenta, la discriminación se vuelve más fina.
La calificación del riesgo de medición tiene implicaciones sobre la probabilidad de que una magnitud esté fuera de control, aun cuando el centro de la distribución caiga dentro de los límites de control.
Cuando IRM = el sistema de medición se comporta como 2 Pasa – No Pasa 3 Bajo – Medio – Alto 4 Muy Bajo – Bajo – Alto – Muy Alto 5 Muy Bajo – Bajo – Medio – Alto – Muy alto

Evidentemente, para una distancia dada del centro al límite de control, la probabilidad de que el valor verdadero caiga fuera del límite aumenta mientras más grande sea la incertidumbre.
Puede ejemplificarse lo anterior suponiendo que los resultados de la medición siguen una distribución normal cuyo centro está separado por h del límite de control.
Es posible determinar la probabilidad de que el valor verdadero caiga fuera del LC cuando el centro de la distribución de la medición esté dentro de los límites de control. O en otras palabras, estamos tratando con la probabilidad de que el valor verdadero esté fuera de los LC si el valor considerado como el más probable está dentro de los LC, en otras palabras, la probabilidad de tomar como bueno el que es malo.
El área sombreada de la figura 7 representa esta probabilidad. Neumann discute la aplicación de conceptos similares en manufactura.
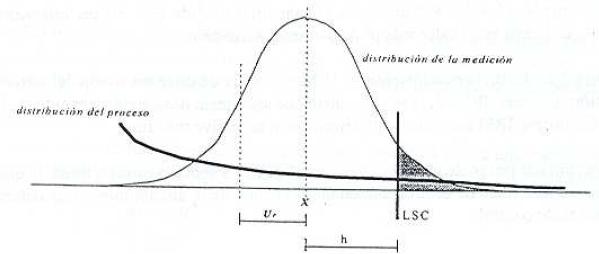
Fuente: Apuntes de Metrología de la UNIDEG
