1. LA RENTABILIDAD ESPERADA DE UNA CARTERA
- Para encontrar la cartera óptima: necesidad de definir la cartera y analizar el rendimiento.
Cartera: fracción de la inversión total en cartera mantenida en cada inversión individual en PF.
PESO CARTERA x( i ) = VALOR DE LA INVERSIÓN ( i ) / VALOR TOTAL DE LA CARTERA
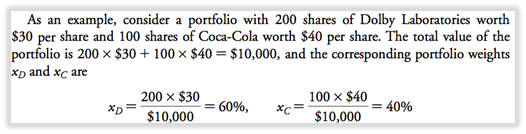
Rendimiento de la cartera: el rendimiento medio ponderado de las inversiones en la cartera.


Rentabilidad esperada de la cartera: el promedio ponderado de la rentabilidad esperada de las inversiones dentro de:
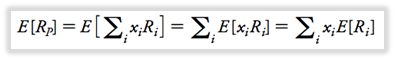
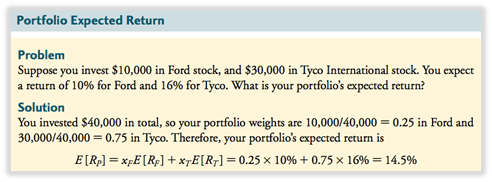
2. LA VOLATILIDAD DE UNA CARTERA DE DOS ACCIONES
DOS FENÓMENOS
1) al combinar acciones en la cartera, reducimos el riesgo a través de la diversificación.
2) la cantidad de riesgo que se elimina en la cartera depende del grado en que las acciones enfrentan riesgos comunes y sus precios se mueven juntos riesgo más común y movimiento diferente = menos riesgoso.
2.1 DETERMINACIÓN DE COVARIANZA Y CORRELACIÓN
Covarianza: producto esperado de las desviaciones de dos retornos de sus medias.


- Si dos acciones se mueven juntas, sus rendimientos tienden a estar por encima o por debajo del promedio al mismo tiempo = la covarianza es positiva.
- Si dos acciones se mueven en direcciones opuestas, una tiende a estar por encima del promedio cuando la otra está por debajo del promedio = la covarianza es negativa.
Correlación: mide cómo se mueven los retornos entre sí; cuantifica la fuerza de la relación.
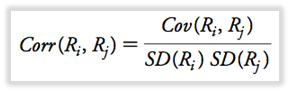
- Interpretación similar como covarianza.
BARÓMETRO DE GRADO DE RIESGO COMÚN COMPARTIDO Y MOVIMIENTO
Correlación +1: perfectamente correlacionada: los rendimientos se mueven juntos como resultado del riesgo común (misma industria).
0 correlación: no correlacionada: los rendimientos no tienen tendencia a moverse juntos o en sentido opuesto (independientes).
-1 correlación: perfectamente no correlacionada: los rendimientos se mueven en direcciones opuestas.
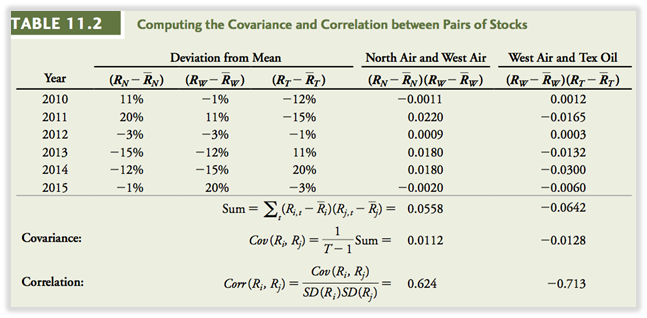
Cada covarianza individual: multiplique ambas desviaciones de la media (ej: 11% * -1% = -0.0011) T-1: todos los años – 1 = 6 – 1 = 5 SD: desviación estándar de cada acción 13,4%.
2.2 CÁLCULO DE LA VARIACIÓN Y LA VOLATILIDAD DE UNA CARTERA


También puede reescribir la ecuación calculando la covarianza de la correlación:
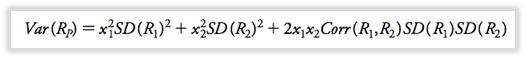
Acción con mayor correlación = mayor varianza y volatilidad.
3. LA VOLATILIDAD DE UNA GRAN CARTERA
3.1 GRAN VARIACIÓN DE LA CARTERA
- La varianza de una cartera es igual a la suma de la covarianza de los rendimientos de todos los pares de acciones en la cartera multiplicada por cada uno de sus pesos de cartera.
La variabilidad general de una cartera grande depende del movimiento conjunto total de las acciones dentro.
3.2 DIVERSIFICACIÓN CON CARTERA IGUAL DE PONDERADA
Cartera igualmente ponderada: cartera en la que se invierte la misma cantidad en cada acción.

- SD (Rp) = RAÍZ DE VAR (Rp).
- SD = volatilidad.
- A medida que n (número de acciones) crece, la volatilidad disminuye.
- La mayor parte de la volatilidad en acciones grandes se elimina como resultado de la diversificación (solo se necesita n=30).
EJEMPLOS: DIVERSIFICACIÓN CON CARTERAS DE IGUAL PONDERACIÓN

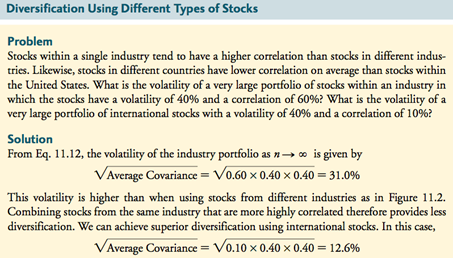

3.3 DIVERSIFICACIÓN CON CARTERAS GENERALES
- Al combinar acciones en una cartera, el riesgo de la cartera será menor que la volatilidad promedio de las acciones individuales.
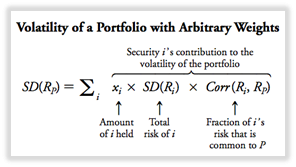

- Rendimiento esperado de la cartera = rendimiento esperado promedio ponderado.
- Volatilidad de la cartera < volatilidad media ponderada.
4. RIESGO VS RENTABILIDAD: ELEGIR UNA CARTERA EFICIENTE
4.1 CARTERAS EFICIENTES CON DOS ACCIONES
- Los inversores quieren baja volatilidad y alto rendimiento esperado -> ambos deben ser considerados.
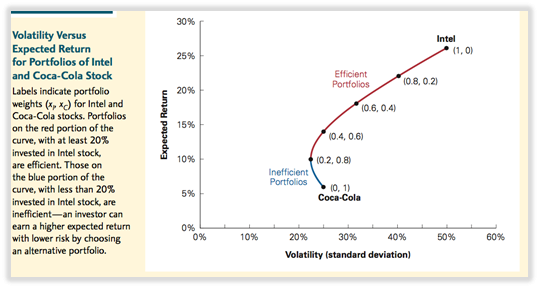
- Solo se deben elegir carteras eficientes porque: 1) mayor rendimiento esperado 2) baja volatilidad AQUÍ: LAS EXISTENCIAS NO ESTÁN CORRELACIONADAS CORRELACIÓN = 0.
IDENTIFICACIÓN DE CARTERAS INEFICIENTES
- Cartera ineficiente: siempre que haya otra cartera que sea mejor en términos de rentabilidad esperada y volatilidad.
IDENTIFICACIÓN DE CARTERAS EFICIENTES
- Carteras eficientes difíciles de clasificar -> los inversores eligen en función de sus preferencias de rentabilidad frente a riesgo.
4.2 EL EFECTO DE LA CORRELACIÓN
- La correlación no tiene efecto sobre el rendimiento esperado, pero sí sobre la volatilidad de la cartera. Cuanto menor es la correlación, menor es el riesgo.
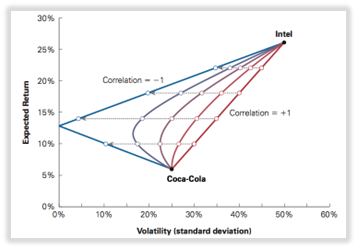
La reducción (&flexión de la curva) se hace mayor a medida que disminuye la correlación -> cuando las dos acciones están perfectamente correlacionadas negativamente = es posible mantener la cartera sin ningún riesgo.
4.3 VENTAS CORTAS
- Hasta ahora solo se consideran carteras en las que se invierte una cantidad positiva.
Posición larga: inversión positiva en seguridad.
Posición corta: inversión negativa en acciones (en venta corta: vende acciones que tomaste prestadas hoy).

- Las ventas en corto solo son rentables si espera que el precio de las acciones baje en el futuro: reciba más por adelantado por las acciones que los costos de reemplazar las acciones de la persona que le prestó.
- Pero: puede ser ventajoso incluso si espera que el precio de las acciones suba siempre que invierta las ganancias de la venta corta en acciones con un rendimiento esperado aún mayor = puede dar lugar a una mayor volatilidad pero ofrece una mayor rentabilidad (atractivo para inversores agresivos).
4.4 CARTERAS EFICIENTES CON MUCHOS ACCIONES
- Para obtener el mejor conjunto posible de oportunidades de riesgo y rendimiento, debemos seguir agregando acciones hasta que se presenten todas las oportunidades de inversión.
- Agregar nuevas oportunidades de inversión y combinar acciones en grandes carteras permite una mayor diversificación y mejora la frontera eficiente.
Frontera eficiente: borde de la región sombreada noroeste; la curva de mayor salida de todas las carteras; todas las carteras en esa curva ofrecen el mayor rendimiento posible para el nivel de volatilidad dado.
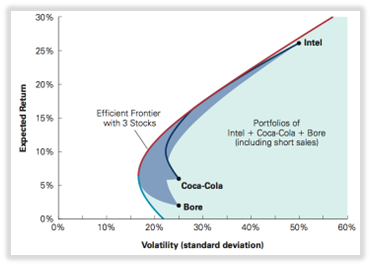
- Zona azul oscuro: carteras sin ventas en corto.
- Área azul claro: carteras con ventas cortas.
- Mejores combis riesgo-rendimiento: en frontera eficiente (curva roja).
- Sumando stocks: (aquí de 2 a 3) mejora la frontera eficiente.
5. AHORRO Y ENDEUDAMIENTO SIN RIESGO
- La capacidad de elegir la cantidad para invertir en valores riesgosos versus libres de riesgo nos permite determinar la cartera óptima de valores de riesgo para un inversionista.
5.1 INVERTIR EN VALORES LIBRES DE RIESGO
- Efecto sobre el riesgo y el rendimiento de poner la fracción x de nuestro dinero en cartera, dejando la fracción restante (1-x) en letras del Tesoro libres de riesgo con un rendimiento de rf.
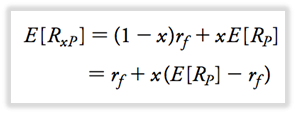
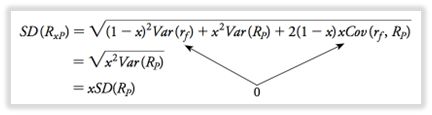
A medida que aumentamos la fracción invertida en la cartera: aumentamos el riesgo y la prima de riesgo proporcionalmente.
- Primera ecuación: el rendimiento esperado es el promedio ponderado de los rendimientos esperados de las letras del Tesoro y la cartera.
- 2ª ecuación: la rentabilidad esperada es igual a la tasa libre de riesgo + fracción de la prima de riesgo de la cartera (ERp-rf).
- La mayor parte de la volatilidad en acciones grandes se elimina como resultado de la diversificación (solo se necesita n=30).
La tasa de interés libre de riesgo es fija y no se mueve con/en contra de la cartera -> volatilidad y covarianza con la cartera = 0.
- Así: la volatilidad es solo una fracción de la volatilidad de la cartera, en función de la cantidad x que invertimos en ella.
5.2 PRÉSTAMO Y COMPRA DE ACCIONES AL MARGEN
- Al aumentar x más allá del 100 %, vendemos al descubierto la inversión libre de riesgo y debemos pagar una rentabilidad libre de riesgo = pedir prestado a la tasa de interés libre de riesgo.
Comprar acciones con margen/usar apalancamiento: pedir dinero prestado para invertir en acciones.
Cartera apalancada: cartera que consiste en posición corta en la inversión libre de riesgo.
- Las carteras con fracción x>100% tienen mayores riesgos y rendimientos que la propia cartera.
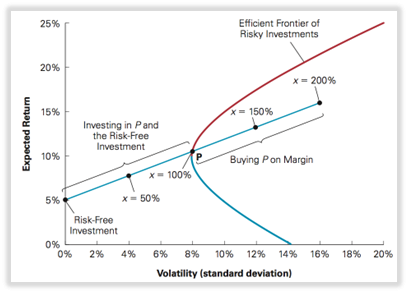

5.3 IDENTIFICACIÓN DE LA CARTERA TANGENTE
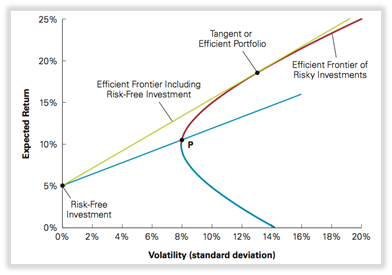
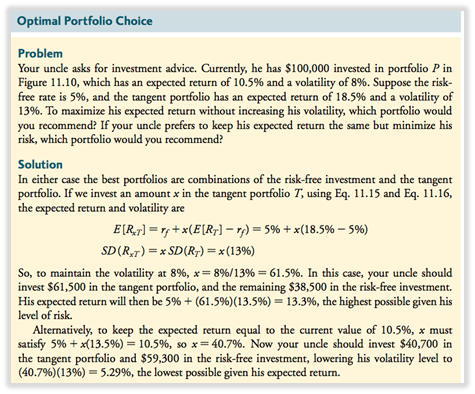
- Para obtener el rendimiento esperado más alto posible para cualquier nivel de volatilidad, debemos encontrar una cartera con la línea más inclinada posible cuando se combina con una inversión libre de riesgo.
Relación de Sharpe: pendiente de la línea a través de una cartera dada; mide la recompensa a la volatilidad proporcionada por la cartera.

Cartera óptima = una con la relación más aguda donde la línea con inversiones libres de riesgo es tangente a la frontera eficiente de inversiones riesgosas.
Cartera tangente/cartera eficiente: cartera con el mayor índice de nitidez , ofrece la mejor rentabilidad por riesgo.
- Todo inversor debería invertir al menos una fracción en la cartera tangente.
6. LA CARTERA EFICIENTE Y LOS RENDIMIENTOS REQUERIDOS
6.1 MEJORA DE CARTERA: BETA Y RENTABILIDAD REQUERIDA
- Mejora de la cartera mediante el aumento de la inversión i en la cartera P depende de:
1) rendimiento esperado que aumenta debido a la inversión en i.
2) rendimiento requerido que es necesario para compensar el riesgo adicional de invertir en i.
beta de la inversión i con cartera P: ßiP mide la sensibilidad de la inversión i a las fluctuaciones de la cartera P -> 1% de cambio en el rendimiento de la cartera desencadena un cambio en el rendimiento de i en ßPi % debido al riesgo de que i tiene en común con P.

- Aumentar la cantidad invertida en i aumentará el índice de nitidez de la cartera P si su rendimiento esperado E( Ri ) excede su rendimiento requerido.
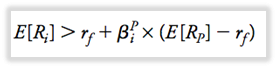
Rendimiento requerido ( r i ): rendimiento esperado que es necesario para compensar la inversión de riesgo i contribuirá a la cartera.
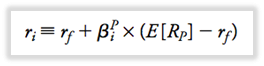

6.2 RENTABILIDAD ESPERADA Y CARTERA EFICIENTE
- Una cartera es eficiente si el rendimiento esperado de cada valor disponible es igual al rendimiento requerido. Reducir o aumentar las tenencias hasta que E( Ri ) = ri.
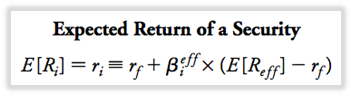
- Reff = rentabilidad de la cartera eficiente (mayor índice de nitidez).
- La prima de riesgo adecuada para una inversión se determina a partir de su beta con la cartera eficiente. Cartera eficiente proporciona un punto de referencia que identifica el riesgo sistemático presente en la economía.
7. EL MODELO DE PRECIOS DE ACTIVOS DE CAPITAL
- El modelo de valoración de activos de capital (CAPM) identifica la cartera eficiente de activos de riesgo sin tener ningún conocimiento del rendimiento esperado de cada valor.
- Usar CAPM para encontrar una cartera eficiente utilizando la cartera de mercado como punto de referencia.
7.1 LOS SUPUESTOS DEL CAPM
1) los inversores pueden comprar y vender todos los valores a precios de mercado competitivos y pedir prestado en rf.
2) los inversores eligen la cartera de valores negociados que ofrece el rendimiento esperado más alto posible dado el nivel de volatilidad que están dispuestos a aceptar.
3) los inversores tienen expectativas homogéneas con respecto a las volatilidades, las correlaciones y el rendimiento esperado de los valores.
7.2 OFERTA, DEMANDA Y EFICIENCIA DE LA CARTERA DE MERCADO
- Como los inversores tienen expectativas homogéneas, identifican la misma cartera como la cartera eficiente y todos exigirán esta (la cartera tangente).
- Ci todos los inversores tienen la cartera tangente, entonces la cartera combinada de valores de riesgo de todos los inversores debe ser igual a la cartera tangente.
- Cada valor es propiedad de alguien, por lo que la suma de la cartera de todos los inversores es la cartera de mercado.
La cartera eficiente/tangente de valores de riesgo (la cartera que tienen todos los inversores) debe ser igual a la cartera de mercado -> la demanda debe ser igual a la oferta.
7.3 INVERSIÓN ÓPTIMA: LA LÍNEA DEL MERCADO DE CAPITAL
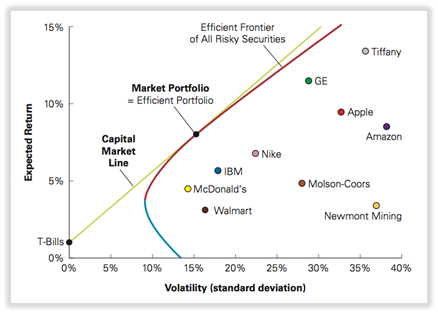
- Cuando se cumplen todos los supuestos de CAPM, la cartera tangente = la cartera de mercado Línea del mercado de capitales: línea tangente desde la inversión libre de riesgo hasta la cartera del mercado.
- Todos los inversores deben elegir una cartera en la línea del mercado de capitales manteniendo una combinación de valores libres de riesgo y cartera de mercado (dependiendo de su preferencia de asumir riesgos).
8. DETERMINACIÓN DE LA PRIMA DE RIESGO
8.1 ESTIMACIÓN DE LA PRIMA DE RIESGO
- Si la cartera de mercado es eficiente, podemos encontrar el rendimiento esperado con beta y reescribir:


Beta(i): beta del valor con respecto a la cartera de mercado.
- Beta de seguridad mide su volatilidad debido al riesgo de mercado en relación con el mercado en su conjunto.
- Para determinar la prima de riesgo apropiada para cualquier inversión, debemos reescalar la prima de riesgo de mercado (cantidad por la cual el rendimiento esperado del mercado excede la tasa libre de riesgo) por la cantidad de riesgo de mercado presente en los rendimientos del valor, medido por su beta con el mercado.

8.2 LA LÍNEA DEL MERCADO DE VALORES VS LA LÍNEA DEL MERCADO DE CAPITAL
Línea del mercado de valores (SML): la línea a lo largo de la cual deben ubicarse todos los valores individuales cuando se trazan de acuerdo con su rendimiento esperado y beta.
Línea de mercado de capitales (CML): representa carteras que combinan la inversión libre de riesgo y la cartera eficiente y muestra el rendimiento esperado más alto que podemos alcanzar para cada nivel de volatilidad; no hay una relación clara entre la volatilidad de las acciones individuales y su rendimiento esperado.
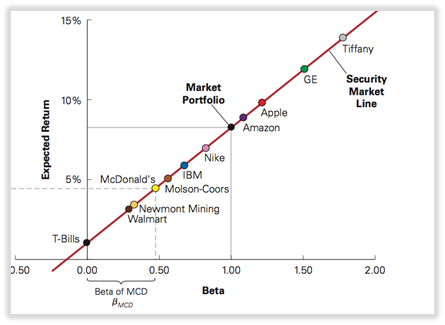
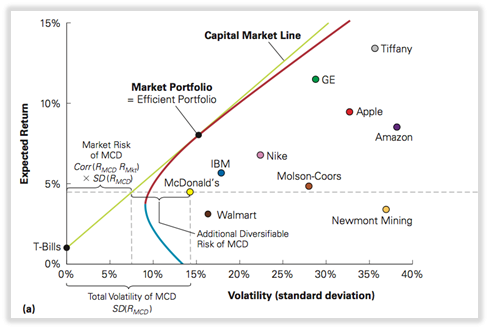
LÍNEA DE MERCADO DE CAPITAL
8.3 BETA DE UNA CARTERA
- Beta de la cartera es la beta media ponderada de los valores de la cartera.



9. ANEXO: EL CAPM CON DIVERSAS TASAS DE INTERÉS
- En la práctica: los inversores reciben una tasa más baja cuando ahorran que la que deben pagar cuando piden prestado.
9.1 FRONTERA EFICIENTE CON DIFERENTES TASAS DE AHORRO Y PRÉSTAMO
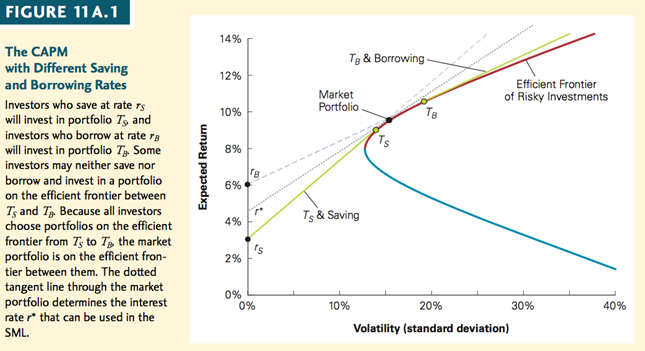
- Ajustando el monto del préstamo, el inversionista puede lograr combinaciones de riesgo y retorno en la línea verde superior.
- Los inversores con diferentes preferencias elegirán diferentes carteras de valores de riesgo = la cartera de mercado ya no es la única cartera eficiente de inversiones de riesgo.
9.2 LÍNEA DEL MERCADO DE VALORES CON TASAS DE INTERÉS DIFERENTES
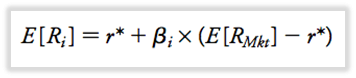
SML todavía se mantiene en esta forma:
- SML se mantiene con alguna tasa r* entre dos tasas diferentes en lugar de rf (tasa de interés libre de riesgo).
- r* depende de la proporción de ahorradores y prestatarios en la economía.
