Elementos de la elipse

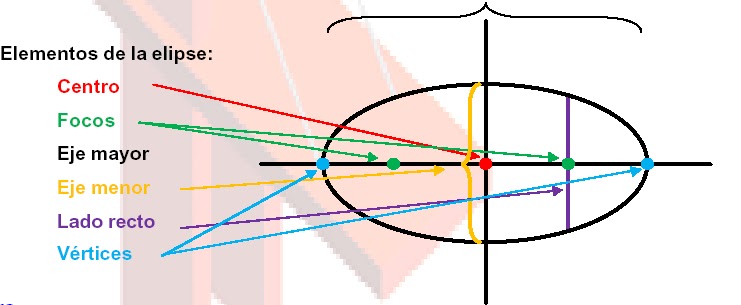
Las elipses poseen los siguientes elementos:

Ejes de simetría. Son perpendiculares en sus puntos medios. El valor del eje mayor AA’ es 2a y el del eje menor BB’ 2b. El punto de intersección de los ejes es el centro de simetría.

Focos. Son dos puntos fijos F y F’, situados sobre el eje mayor y simétricos respecto al eje menor. FF’ es igual a 2c.

Radios vectores. Son los segmentos comprendidos entre los puntos de la elipse y los focos. La suma de los radios vectores correspondientes a un mismo punto es igual a 2a.

Circunferencia principal. Es la que tiene su centro en el centro de la elipse y radio igual al semieje mayor.

Circunferencias Focales. Son las circunferencias con centro en los focos y radio igual a 2a.

La elipse es una curva cerrada y plana. Se define como el lugar geométrico de los puntos del plano cuya suma de distancias a dos puntos fijos, llamados focos, es constante e igual al eje mayor 2a.

Sea Pn un punto cualquiera de la elipse, se cumple que:

PnF + PnF’ = 2a

Para determinar los focos F y F’ de una elipse conocidos los ejes, se hace centro en un extremo del eje menor, B por ejemplo, y se traza un arco de radio igual al semieje mayor a. La intersección del arco con el eje mayor son los focos de la elipse.

Sabiendo que B es un punto de la elipse, se cumple que:

BF + BF’ = 2a, como BF=BF’, por estar B en un eje de simetría, resulta que BF=BF’=a.

Fuente: Apuntes de Geometría descriptiva de la Universidad de Londres