Estadística descriptiva

La estadística descriptiva es la explicación del comportamiento de una población basándose en un conjunto de datos. Las medidas clave a considerar de la estadística descriptiva son la media y la desviación estándar.

Media de la población: la media (o promedio) de la población es la suma de todos los datos, divididos entre el número de datos. Esta es la medida más utilizada en la estadística tanto descriptiva como inferencial.

– Notación: se denota por la letra griega μ
– Fórmula:

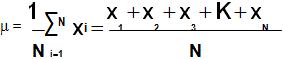
La media es la medida de mayor representatividad de la población, sin embargo, hay que tener cuidado con ella, porque a veces puede ser afectada por valores extremos.

Desviación estándar: la otra medida de gran importancia en la estadística descriptiva es la desviación estándar. Esta podría definirse como la medida de la dispersión de los datos con respecto al promedio. Permite ubicar que tan buena es la aproximación que da el promedio ya que a menor desviación estándar, menor es la diferencia entre los datos.

– Notación: se denota por la letra griega σ.
– Fórmula:

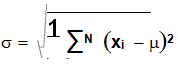
Media de la muestra: esta es la medida más utilizada en la estadística. Esencialmente es igual a la media de la población sólo que ahora tomando los datos de la muestra, es decir, la media de la muestra es la suma de todos los datos de la muestra, divididos entre el número de datos.

– Notación: se denota por una X con una línea por encima de ella y se lee como equis barra. ¯X
– Fórmula: la única variación que sufrirá la fórmula es que en lugar de considerar N datos, se tomarán en cuenta n (por tradición N es el tamaño de la población y n es el tamaño de la muestra).

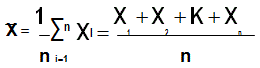
Desviación estándar: también podemos calcular la desviación estándar de la muestra que también se define como la medida de la dispersión de los datos con respecto al promedio o media muestral. Al igual que la poblacional permite ubicar que tan buena es la aproximación que da el promedio ya que a menor desviación estándar, menor es la diferencia entre los datos. Hay sin embargo una pequeña variación que vale la pena mencionar en el cálculo de la desviación estándar y es que a diferencia de la poblacional la suma de los cuadrados de la diferencia de los datos observados menos la media no se divide entre n, sino entre n-1. Esto se debe al concepto de grados de libertad que se defina como el número de variables aleatorias menos las restricciones en un experimento; en este caso hay n variables aleatorias y una restricción, que es precisamente que la información se obtendrá de esa muestra.

– Notación: se denota por la letra s.
– Fórmula:

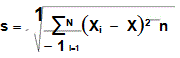
Fuente: Apunte de Pronósticos de la Unideg