Aquí la cosa es un poco distinta, aunque la base del cálculo de tramas que hará la máquina será el mismo.
La resolución «ideal» de un semitono
Una imagen de semitonos ya tiene una resolución por si misma. Este no era el caso de los textos o dibujos vectoriales de línea (y las imágenes digitales de línea de buena calidad suele tener una resolución tan elevada que se puede descontar ese factor).
El caso perfecto, una relación entre píxeles y puntos de semitono.
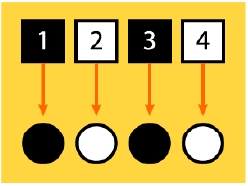
En un mundo ideal, la perfecta reproducción se conseguiría en una imagen que pusiera un píxel de información para formar cada punto de semitono, ni más ni menos.
Esa relación, además ahorrará muchos cálculos al RIP y facilitará la impresión de la imagen.
![]()
Pixelización de la imagen: Un mismo pixel para dos puntos (o más) de semitono. Aparecerán dentados y «cuadraditos».
Los problemas empiezan a aparecer cuando para formar nuestros puntos de semitono no tenemos al menos esa relación de un píxel por punto de trama.
Eso quiere decir que los puntos de trama empezarán a repetir valores de píxeles. Aparecerán los temibles bordes dentados en los contornos de la imagen (inglés: jaggies) y los cuadraditos.
La imagen aparecerá pixelizada porque el RIP carecerá de datos de imagen suficientes para formar esa imagen de calidad ideal de un píxel por punto de trama.
Sin embargo, en algunos dispositivos que dispongan de un RIP verdaderamente bueno, éste puede hacer una cierta interpolación y «deducir» los píxeles faltantes, promediando los de la vecindad (del mismo modoe que puede hacerlo Photoshop).
Ahora bien, esto no «inventará» los píxeles que falten, sólo los fingirá.
Exceso de píxeles
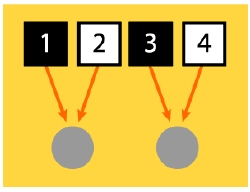
Exceso de píxeles: un pixel blanco y uno negro quedan promediados en un mismo punto de semitono.
Por cierto, si quieres saber qué ocurre cuando hay más de un píxel para cada punto de semitono, te diré que lo que el RIP hace es promediar los valores de los píxeles participantes y darle el valor resultante al punto de semitono en cuestión.
Eso provoca valores «intermedios» que pueden provocar cierta «borrosidad» o suavidad en la transición de zonas de distintos tonos o luminosidad.
La cuestión clave, entonces es: ¿Y cómo saber cual es la resolución que nos asegura al menos un pixel por cada punto de semitono? ¿Existe una forma de saberlo?
Pues sí. En principio es simple: Si vamos a imprimir una imagen a una lineatura de 100 lpp, esto quiere decir que en una línea recta habrá 100 puntos de semitono.
Entonces bastaría una imagen con una resolución de 100 ppp. Ahora bién, este cálculo presupone que las tramas tienen un ángulo 0. Es decir, que no están tumbadas.
Pero en la vida real sabemos que las tramas deben girarse para que su presencia sea poco evidente al ojo. La trama que más girada está con respecto al ángulo 0, es la negra (el color más oscuro y el más evidente al ojo).
La trama menos girada es la amarilla (cuya presencia es de por si poco evidente, de hecho está en grado 0).
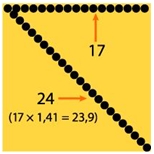
La vieja regla de la diagonal del cuadrado = lado multiplicado por la raiz cuadrada de dos.
De ese modo, la trama negra forma la diagonal de ese cuadrado de 100 lpp y mide, obviamente algo más. Ese algo es fácil de saber, ya que (matemáticas de primaria) la diagonal de un cuadrado es igual al lado por la raiz cuadrada de 2.
Entonces, para asegurarnos esa relación pixel-trama de 1:1 debemos multiplicar la lineatura (el lado del cuadrado formado por una pulgada) por la raiz cuadrada de 2 (que es aproximadamente 1,41). En nuestro ejemplo sería: 100 × 1,41 = 141 ppp
(redondeamos si queremos a 150 ppp.
Fuente: Apunte de Organización de presentaciones y exhibiciones de la U de Londres
