¿Recuerdas cómo empezaste a aprender números?
Seguramente no, pero aunque no lo recuerdes te puedo asegurar que iniciaste con los números que en matemáticas se llaman el conjunto de los números naturales.
Todos empezamos el aprendizaje de las matemáticas de la misma manera: contando con nuestros dedos desde el uno al tres, después al cinco y más tarde al diez.
Y así, poco a poco entendimos que hay más y más números, y que podríamos pasar la vida contando y contando, y nunca terminaríamos porque el conjunto de números natural es es infinito.
En matemáticas el conjunto de los números naturales se denota de la siguiente manera:
N = {1, 2, 3… ∞}
El símbolo ∞ se llama infinito y los tres puntos suspensivos representan todos los números mayores que tres, que (obviamente) no podemos escribir porque nunca terminaríamos.
Al ir creciendo vamos ampliando nuestro conocimiento sobre los números y aprendemos que podemos representar ausencia de objetos (o vacío) mediante el número cero, y entendemos que con números negativos se pueden representar gran cantidad de situaciones (temperaturas bajo cero, niveles de profundidad bajo la superficie de la tierra, saldos deudores en cuentas bancarias).
Esta familia de números se llama números enteros y este conjunto se representa de la siguiente manera:
Z = {-∞ … -3, -2, -1, o, 1, 2, 3 … ∞}
Como puedes ver, el conjunto de los números naturales está contenido en el conjunto de los números enteros.
Poco a poco se van haciendo más complejos los conjuntos de números. Después se tuvo la necesidad de representar las partes de un entero (media manzana, un cuarto de kilo de sal, un tercio de tablilla de chocolate), y así nacieron las fracciones que son parte de los números racionales.
El conjunto de los números racionales es el conjunto de todos los números x tales que pueden ser representados como cociente de dos enteros, siempre y cuando el denominador de ese cociente sea diferente de cero.
El conjunto de los números racionales se representa de la siguiente manera
Aquí x representa cualquier número racional, a y b son los números enteros de los que habla la definición anterior y la barra vertical posterior a x en matemáticas se lee “tal que”.
Al final se establece que el denominador del cociente debe ser distinto de cero.
Ejemplos de números racionales son:
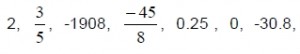
ya que todos ellos se pueden representar como el cociente de dos números enteros cuyo denominador es diferente de cero.
Hasta aquí, los números de los que hemos estado hablando nos son muy familiares porque los usamos en la vida cotidiana, pero existe otro conjunto de números que no nos son tan familiares, ni son famosos; ese es el conjunto de los números irracionales.
El conjunto de los números irracionales se denota por Ι, y está formado por el conjunto de números que no pueden ser representados como el cociente de dos enteros.
Ejemplos de números irracionales son:
![]()
y el número e= 2.718281… ,por supuesto que no son todos, existe una infinidad de números irracionales, y aunque son menos usados que los naturales, enteros o racionales, son tan importantes como todos ellos.
La característica común entre números racionales y números irracionales es que pueden ser escritos como decimales; los números racionales son decimales finitos o infinitos periódicos , mientras que los números irracionales son decimales infinitos no periódicos.
Ejemplos:
1 es un número racional porque puede escribirse como 1.00000… (período cero)
3.5 es un número racional porque es decimal finito.
-8.002 es un número racional porque es decimal finito.
∏ = 3.141592654… es un número irracional porque es decimal infinito no periódico
2 = 1.4142135… es un número irracional porque es d ecimal infinito no periódico
9 = 3 es racional.
Finalmente, el conjunto de los números reales reúne a todos los conjuntos anteriores, y se representa por.
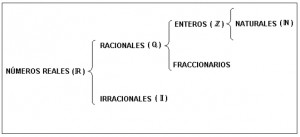
Los conjuntos de números están relacionados, los naturales están contenidos en los enteros, y estos a su vez están contenidos en los racionales, la unión de números racionales e irracionales forman el conjunto de los números real es.
Fuente: Apunte de matemáticas básicas de la UNIDEG.
