Magnitudes fundamentales y magnitudes derivadas

Dado que, como hemos visto, las relaciones mediante las que se expresan las leyes fundamentales que obtiene la física acerca del comportamiento de la materia se basan en la medición de las variaciones de ciertas cantidades o propiedades, es, pues, necesario disponer de un numero de cantidades lo más reducido posible que permitan obtener las demás, así como reducir la expresión de dichas magnitudes a un cierto número de cantidades.

Este es el criterio que permite distinguir entre  magnitudes fundamentales y magnitudes derivadas. Las primeras son aquellas que no pueden derivarse de ninguna otra y constituyen la base de los sistemas de medida empleados en la física.

Son la longitud, indicada mediante I, la masa, que se expresa por m, y el tiempo, que se indica mediante t.  Sin embargo, la elección de dichas magnitudes se deriva de consideraciones de orden práctico y no implica que éstas representen propiedades fundamentales de la energía o la materia.

Por el contrario, las magnitudes derivadas son aquéllas que se obtienen a partir de las fundamentales por combinación de ellas o el como consecuencia de la si aplicación de las leyes físicas.

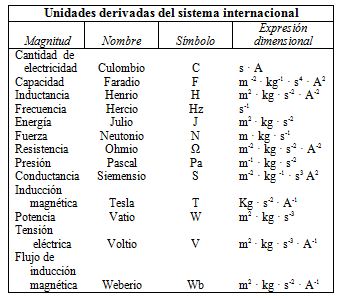
Así, por ejemplo, la velocidad es la relación entre la longitud y el tiempo, como ya hemos visto, siendo las unidades que se emplean para expresarla el metro/segundo.