Método dual simplex

En cualquier iteración primal Zj – Cj, el coeficiente de la función objetivo de Xj, es igual a la diferencia entre el primero y segundo miembro de la restricción dual asociada.

cuando, en el sentido de la maximización, la iteración primal no es optima, Zj – Cj < 0 por lo menos para una variable. solo en el optimo tenemos Zj – Cj > 0 para todas las j.

Analizando esta condición desde el punto de vista de la dualidad, se tiene:

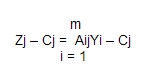
por lo tanto, cuando 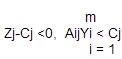, significa que el dual es infactible

Cuando el primal es no optimo. por otra parte, cuando 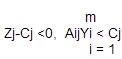, Indica que el dual se vuelve factible cuando el primal alcanza la optimidad.

Estos resultados sugieren un nuevo método de solución para programas lineales, que comienza infactible pero (mejor que) optima.

El nuevo método, llamado simplex dual, conservara la optimidad y las iteraciones sucesivas trabajaran para anular la infactibilidad.

Cuando se llega a la factibilidad. Cuando se llega a la factibilidad, el proceso termina porque la solución es factible y óptima.

Este tipo de problema se encuentra en ciertos modelos de pl; pero lo que es mas importante es que se utiliza en forma directa para realizar el análisis de sensibilidad.

Fuente: Apunte de Investigación de Operaciones del Instituto Tecnológico de la Paz