Regresión lineal
Con mucha frecuencia es necesario resolver problemas que implican conjuntos de variables, cuando se sabe que existe una relación inherente entre ellos.
A menudo se tiene una sola variable dependiente o respuesta (conocida como efecto) y la cual no se controla en el experimento. Esta variable tradicionalmente se denota como Y.
Esta respuesta depende de una o más variables independientes o de regresión (causas) que se denotan normalmente como X1, X2,…,XK.
Estas variables causa se miden en general con un error despreciable y en realidad, en la generalidad de los casos, se controlan en el experimento.
Regresión lineal simple
La regresión lineal simple nos presenta el caso cuando sólo existe una variable de regresión (causa) independiente X y una sola variable aleatoria independiente Y.
El concepto de lineal surge dado que la relación entre estas variables puede interpretarse como aquella que tienen las variables en la ecuación de una recta.
Ecuaciones de regresión
Las ecuaciones de la regresión se van a obtener mediante el método de los mínimos cuadrados que básicamente lo que hacen es minimizar el error de fallar en el pronóstico.
La idea consiste en minimizar el valor del MSE y a partir de ahí escoger la mejor ecuación que represente los datos.
En general lo que sucede es que se tiene un conjunto de datos que al graficarlos en un diagrama de dispersión se presentarían de esta forma:
Diagrama de dispersión
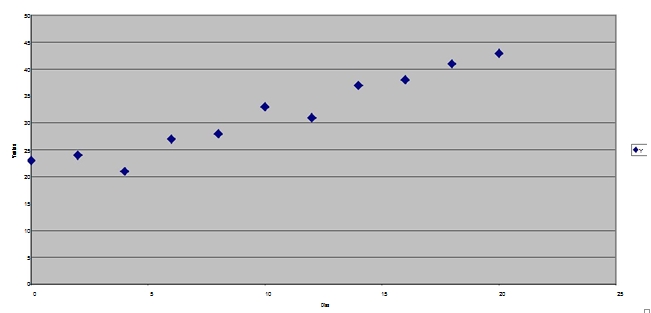
La intención de este método es encontrar la recta que mejor se aproxime a este cada uno de los datos, o en otra palabras, que mejor representen la relación entre estos puntos.
Lo que se va a hacer es encontrar la ecuación de la recta más representativa de estos datos.
Formula:
![]()
En el caso de la regresión se va a tener información histórica de los valores de y a determinados valores de x.
Se usaran dichos valores para encontrar los valores de a y b que minimizan el error y aproximan más cualquier recta al conjunto de datos.
Esto valores son llamados los coeficientes de regresión y que es lo que se busca.
Una vez encontrados estos valores se usa esta ecuación de regresión para pronosticar y a diferentes valores de x.
El método para encontrar a y b requiere del uso de derivadas parciales.
Formula:
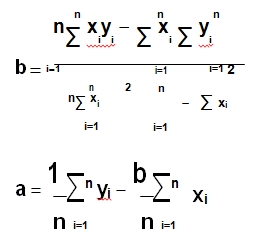
La ecuación de regresión sería entonces:
![]()
Fuente: Apunte de Pronósticos de la Unideg.
