Métodos de evaluación que toman en cuenta eI valor del dinero a través del tiempo

El estudio de la evaluación económica es la parte final de toda la secuencia de análisis de la factibilidad de un proyecto.

Si no han existido contratiempos, se sabrá hasta este punto que existe un mercado potencial atractivo; se habrán determinado un lugar óptimo para la localización del proyecto y el tamaño más adecuado para este último, de acuerdo con las restricciones del medio; se conocerá y dominará el proceso de producción, así como todos los costos en que se incurrirá en la etapa productiva, además de que se habrá calculado la inversión necesaria para llevar a cabo el proyecto.

Sin embargo, a pesar de conocer incluso las utilidades probables del proyecto durante los primeros cinco años de operación, aún no se habrá demostrado que la inversión propuesta será económicamente rentable.

En este momento surge el problema sobre el método de análisis que se empleará para comprobar la rentabilidad económica del proyecto. Se sabe que el dinero disminuye su valor real con el paso del tiempo, a una tasa aproximadamente igual al nivel de inflación vigente.

Esto implica que el método de análisis empleado deberá tomar en cuenta este cambio de valor real del dinero a través del tiempo. También se analizarán las ventajas y desventajas de los métodos de análisis que no toman en cuenta este hecho.

Antes de presentar los métodos, se intentará describir brevemente cuál es la base de su funcionamiento. Supóngase que se deposita una cantidad P en un banco, en la misma forma que se invierte cierta cantidad de dinero en una empresa.

La cantidad se denota por la letra P, pues es la primera letra de la palabra presente, con lo que se quiere evidenciar que es la cantidad que se deposita al iniciar el periodo de estudio o tiempo cero (to).

Esta cantidad, después de cierto tiempo de estar depositada en el banco o invertida en una empresa, deberá generar una ganancia a cierto porcentaje o de la inversión inicial P.

Si de momento se le llama » i « a esa tasa de ganancia y «n» al número de periodos de tiempo en que ese dinero gana la tasa de interés » i «, «n» sería entonces el número de periodos capitalizables.

Con estos datos, la forma en que crecería el dinero depositado en un banco, sin retirar los intereses o ganancias generados sería:

En el primer periodo de capitalización (n = 1), generalmente un año, denominando F (futuro) a la cantidad acumulada en ese futuro:

F 1 = P + Pi = P (1 + i ) = P (1 + i )

en el periodo n = 2, la cantidad acumulada hacia el fin de año sin retirar la primera ganancia Pi sería la cantidad acumulada en el primer periodo (P + Pi), más esa misma cantidad multiplicada por el interés que se gana por periodo:

Siguiendo el mismo razonamiento para encontrar F 1 y F 2 (sin que se hayan retirado los intereses), la cantidad acumulada en un futuro, después de n periodos de capitalización, puede expresarse como:

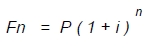
Esto introduce el concepto de equivalencia. Si se pregunta a cuánto equivalen $ 1,000 de hoy a $ 1,000 dentro de un año, es cierto suponer que con base en la fórmula, para calcular cantidades equivalentes del presente al futuro, y sabiendo que P = 1,000 (cantidad en tiempo presente) y n = 1, la cantidad equivalente de $ 1,000 dentro de un año dependerá exclusivamente de la «i“ o tasa de interés que se aplique.

Tómese una tasa de referencia; por ejemplo, la tasa inflacionaria. En México, hacia 1985, esta tasa fue cercana a 90% ( i = 0.9) entonces:

F 1 = I,000 (1 + 0.9) = I,900

Fuente: Apunte Elaboración y evaluación de proyectos de la Unideg