Vamos a calcular el tamaño del lote a través de la aplicación del modelo determinístico de Harris:
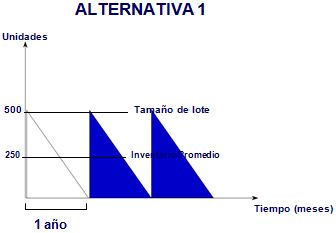
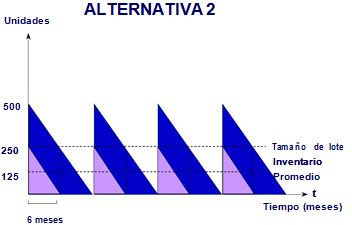
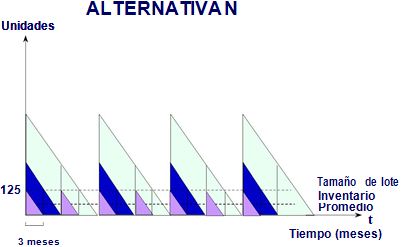
De las gráficas anteriores se puede deducir lo siguiente:
Si T es grande, q (tamaño del lote) también lo es y el costo de almacenamiento es grande. En cambio n es pequeño, pues hay que hacer pocos pedidos.
Si T es pequeño, q (tamaño del lote) también lo es y el costo de almacenamiento es pequeño. En cambio n es grande, pues hay que hacer muchos pedidos.
Variables del modelo
R = Necesidades totales
C1 = Costos de pedir
C2 = Costos de mantener
q = Tamaño del pedido
n = Número de pedidos
q/2 = Inventario promedio
1 = Costo total de pedir
2 = Costo total de mantener
T = Costo total (Costo de pedir + costo de mantener)
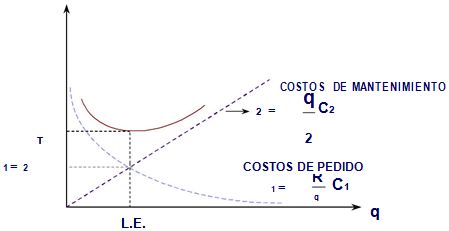
Donde:

En el nivel óptimo los dos costos son iguales.
Costo de hacer pedidos = Costo de mantenimiento
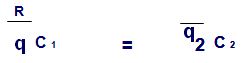
Fuente: Apuntes de Costos y presupuestos de la FCA de la UNAM
