Operaciones con fracciones

Las fracciones son parte de los números racionales.

Partes de una fracción:

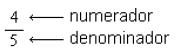
Suma y resta de fracciones.

Cuando las fracciones a sumar, o restar, tienen el mismo denominador el resultado será una fracción con denominador igual al de las fracciones que se suman, o restan, y numerador igual a la suma, o resta , de los numeradores de las fracciones iniciales, esto es:

Suma y resta de fracciones con diferente denominador.

Cuando las fracciones a sumar, o restar, no tienen el mismo denominador el resultado se encuentra mediante los siguientes pasos:

1)  Se calcula el mínimo común múltiplo (m.c.m.) de los denominadores de las fracciones a sumar o restar.

2)  El mínimo común múltiplo es dividido por cada un o de los denominadores de las fracciones involucradas en la operación, y ese resultado se multiplica por el numerador de la fracción que le corresponde.

3) Finalmente, el resultado será una fracción con denominador igual al mínimo común múltiplo de todas las fracciones involucradas , y denominador igual a la suma, o resta, de los resultados calculados en el inciso anterior.

Ejemplo.

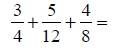
1)  El m.c.m. de los denominadores de las fracciones involucradas en la suma es 24.

2)  Dividimos el m.c.m. por cada uno de los denominadores de las fracciones

y ese resultado se multiplica por el numerador de la fracción correspondiente

3) Finalmente el resultado es

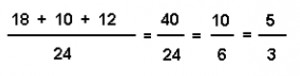
Nota: En algunas ocasiones el cálculo del m.c.m. es tardado, en esos casos se puede utilizar el producto de los denominadores de todas las fracciones involucradas en vez del m.c.m.

Multiplicación de fracciones.

Para multiplicar dos fracciones debes multiplicar numerador por numerador y denominador por denominador (obedeciendo la ley de los signos) como indica el ejemplo siguiente.

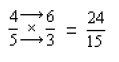
Ejemplo:

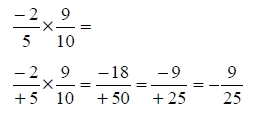
División de fracciones.  La división  de  fracciones no es tan directa como la multiplicación, la siguiente figura te muestra como se dividen dos fracciones.

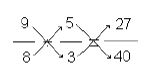
Para dividir dos fracciones multiplica el numerador de la primera fracción por el denominador de la segunda, eso nos da el numerador del resultado.

Después multiplicar el denominador de la primera fracción por el numerador de la segunda, eso nos dará el denominador del resultado.

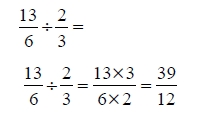
Operaciones con números mixtos. ¿Qué sucede cuándo se nos presentan problemas como el siguiente?: “en una distribuidora de productos químicos se desea saber qué cantidad de cloro se tiene en existencia”.

Si el encargado tiene anotado en su inventario: un garrafón y medio en la tienda, tres garrafones un cuarto en bodega y dos garrafones un tercio en el sótano, ¿cuánto cloro se tendrá en total?.

La operación que tendrá que realizar el encargado e s la siguiente:

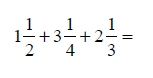
Nota:Cada uno de los términos, se llaman fracciones mixtasdebido a que tienen una parte fraccionaria y una parte entera.

Operaciones como la suma (1) se reducen a una operación de fracciones simples convirtiendo los enteros de cada fracción mixta a fracciones con el mismo denominador de la parte fraccionaria, esto es, en el primer término de la suma anterior todo se convierte a medios, en el segundo término todo se convierte en cuartos y en el tercer término todo se convierte en tercios.

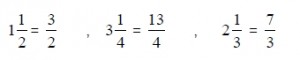
Estas conversiones se pueden realizar mentalmente, pero existen casos en que la conversión lleva más tiempo y por ello es conveniente aprender la regla de conversión y aplicarla.

Regla de conversión de fracciones mixtas a fracción es simples.

Para convertir una fracción mixta a una fracción simple se multiplica el denominador de la parte fraccionaria, por la parte enteray el resultado de éste producto se suma al numerador de la parte fraccionar; la fracción resultante deberá tener como numerador el resultado obtenido en el proceso anterior y denominador igual al de la parte fraccionaria inicial.

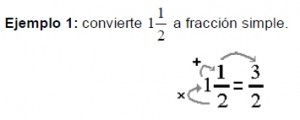
Fuente: Apunte de matemáticas básicas de la UNIDEG.