Potencia de un punto respecto a una circunferencia

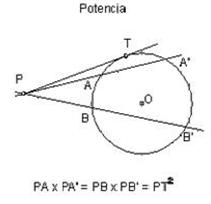
Si trazamos un haz de rectas secantes desde un punto P a una circunferencia, el producto de los segmentos comprendido entre el punto P y los puntos de intersección de las rectas con la circunferencia.

La potencia es igual al cuadrado de la distancia del punto P, al punto de tangencia de una recta tangente a la circunferencia, trazada desde P. 

PA x PA’ = PB x PB’ = … = PN x PN’ = PT²

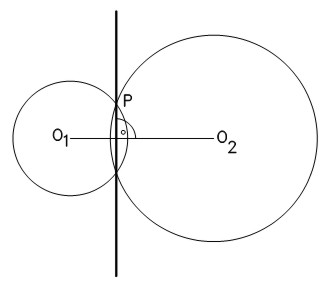
Eje Radical es el lugar geométrico de los puntos que tienen igual potencia respecto a dos circunferencias. El eje radical de dos circunferencias secantes, es la recta que une los puntos de intersección de ambas circunferencias.

El de dos circunferencias tangentes, es la recta tangente común a ambas circunferencias en el punto de tangencia.

Para hallar el eje radical de dos circunferencias exteriores se traza una circunferencia auxiliar secante a las dadas. Por el centro radical de las tres circunferencias trazamos una perpendicular a la recta que una los centros de las circunferencias exteriores.

Centro Radical es el punto que tiene igual potencia respecto a tres circunferencias. Se encuentra en la intersección de los ejes radicales de las circunferencias tomadas dos a dos.

La mayoría de los problemas de tangencia se resuelven aplicando los conceptos de lugares geométricos, por suma y diferencia de radios, y por potencia.

Se pueden pedir rectas tangentes a circunferencias, o circunferencias tangentes a rectas y, o circunferencias. Cuando se piden circunferencias, se pueden fijar tres condiciones, pasar por un punto, ser tangente a una recta y ser tangente a otra circunferencia.

La combinación de estas tres condiciones nos dan 10 casos, que se representan por combinación de las iniciales P, R, y C. Cuando no se fijan las tres condiciones es necesario dar algún dato, como el radio o los puntos de tangencia.

Fuente: Apuntes de Geometría descriptiva de la Universidad de Londres