Resolución de ecuaciones de primer grado con una incógnita

Resolver una ecuación es hallar sus raíces, o sea el valor o los valores de las incógnitas que satisfacen la ecuación.

Para resolver una ecuación se deben tener en cuenta las siguientes reglas.

1) Si a los dos miembros de una ecuación se suma una misma cantidad, positiva o negativa, la igualdad subsiste.

2) Si a los dos miembros de una ecuación se resta una misma cantidad, positiva o negativa, la igualdad subsiste.

3) Si los dos miembros de una ecuación se multiplica por una misma cantidad, positiva o negativa, la igualdad subsiste.

4) Si los dos miembros de una ecuación se dividen por una misma cantidad, positiva o negativa, la igualdad subsiste.

5) Si los dos miembros de una ecuación se elevan a una misma potencia o si a los dos miembros se les extrae raíz, la igualdad subsiste.

Veamos como se aplican las reglas anteriores.

Resolver   5x +1 = 6

Solución: Nos piden hallar el valor de x que verifique la igualdad, entonces debemos despejar x , es decir, dejarla sola en un miembro. Vemos que en la ecuación 5x + 1 = 6 debemos quitar el 1 para ir despejando x , entonces podemos aplicar la regla dos y restar a ambos miembros –1 y no habremos alterado la igualdad.

5x +1 – (1) = 6 – (1)
5x = 6 -1
5x = 5

Pareciera como si para quitar +1 del primer miembro lo pasáramos restando al segundo miembro.

Ahora, a x le estorba el 5 para quedar sola en el primer miembro. Aplicamos la regla cuatro y dividimos ambos miembros por 5, de esa forma tenemos

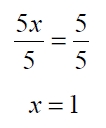
Pareciera como si para quitar el 5 del primer miembro lo pasáramos dividiendo al segundo miembro, y de esa forma despejamos x y hallamos su valor.

La solución de la ecuación es x = 1

Verificación de la solución

La verificación de la solución es muy importante, si x = 1 es solución entonces al sustituirla en esta deberá cumplirse la igualdad.

5x +1 = 6
5(1) + 1= 6
6 = 6

por tanto  x = 1 sí es solución de la ecuación.

Resolver 5x = 8x -15

Solución: Nos piden hallar el valor de x que verifique la igualdad, entonces debemos despejar x , pero como x está en ambos miembros debemos pasar todas las equ is a uno solo, digamos el primer miembro, para esto restemos a ambos miembros 8x y así tendremos

5x – 8x = 8x -15 – 8x5x – 8x = -15 -3x = -15

Pareciera como si para quitar 8x, que está sumando en el segundo miembro, lo pasáramos restando al primer miembro.

Ahora, dividamos por – 3 ambos lados de la igualdad

x= 5

Pareciera como si para quitar –3, que está multiplicando en el primer miembro, lo pasáramos dividiendo al segundo miembro.

Fuente: Apunte de matemáticas básicas de la UNIDEG.