Suma lógica

Como hemos visto, trabajamos sobre la base de dos números, el 1 y el 0, por lo que decimos que el sistema de numeración empleado es binario. Si bien la representación de los números en el sistema decimal (de base 10) al que estamos acostumbrados es mucho más corta, tiene la desventaja de que no emplea exclusivamente los dígitos 0 y 1, que, como sabemos, son los que necesitamos para poder aplicar las tablas de verdad correspondientes a las operaciones (o circuitos) propuestos.

Por ello cabe buscar un método que permita pasar de la numeración decimal a la binaria a fin de poder realizar las operaciones binarias con la ayuda de circuitos de conmutación, fundamento  del empleo de los ordenadores electrónicos como máquinas aritméticas. Los datos, sean del tipo que sean, pueden tratarse de forma manual, mecánica o electrónica. El último tipo de tratamiento de los datos, que es el que nos interesa aquí, requiere un proceso de recopilación y selección así como de almacenamiento y  procesamiento.

Los datos almacenados en los ordenadores no se conservan en su forma primitiva sino que se codifican en sistema binario (dos posibilidades contrarias, positivo o negativo, abierto o cerrado, etc,), forma de representación muy sencilla y segura que ofrece asimismo la ventaja de no tener que emplear las diez cifras del sistema decimal sino tan sólo las dos base del binario o dual (el 0 y el 1). Desde el punto de vista del sistema físico dichos valores se representan mediante la magnetización positiva o negativa, en la memoria, de núcleos magnéticos o soporte de datos, existencia o no de un impulso, etc.

Dado que disponemos de tan sólo dos dígitos diferentes, la representación de un número en el sistema dual es más larga que en el decimal. En este último (que es posicional), la posición que ocupa el dígito indica su valor relativo, siendo el coeficiente de una cierta potencia de 10, (la base del sistema de numeración). Cada una de dichas potencias recibe el nombre de unidades (l0°), decenas (10¹), centenas (10²), millares (10³), etc.

Por el contrario, en el sistema dual el valor de la cifra no está definido por su potencia de 10 sino por su potencia de 2; o sea que 1, 2, 4,

etc., corresponden a 2⁰, 2¹, 2², etc.

De este modo, un número cualquiera, que en el sistema decimal está compuesto por tantas unidades, tantas decenas, tantas centenas, en el binario esta formado por potencias de 2. Supongamos el ejemplo: 89, que en el sistema decimal esta compuesto por 9 unidades y 8 decenas. En el sistema dual su descomposición seria (en potencias de 2) como

Sigue:

Resumiendo los coeficientes de las potencias de 2 correspondientes a este número obtenemos 1011001, expresión en el sistema de base 2 del número 89.

El método para llevar a cabo la transformación de los números decimales en números binarios es muy sencillo: supongamos nuevamente el número 89. Si lo dividimos en 2 nos da 44, con un resto igual a 1; si volvemos a dividirlo por 2 obtenemos 22, sin resto; si continuamos el proceso de división sucesiva por 2 obtenemos finalmente la siguiente tabla:

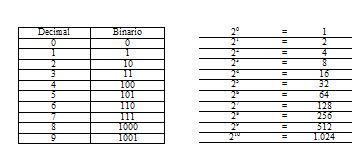
y leyendo los restos desde abajo hacia arriba obtenemos nuevamente, 1011001, que es la expresión de 89 en el sistema dual. Para seguir el camino inverso, es decir, transformar los números binarios en números expresados e el sistema decimal, el camino que se sigue es también el inverso.

Para ello se toma la expresión del número binario en cuestión, 1011001, y se desarrolla de la manera siguiente:

que es:

Una vez visto el método para pasar de números decimales a binarios y viceversa, vamos a ocuparnos de cómo deben llevarse a cabo las operaciones con números binarios.

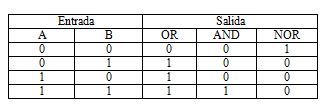
La representación dual presenta la ventaja de que las operaciones son mucho más sencillas ya que la suma, por ejemplo, responde a las siguientes reglas;

De este modo, la suma de dos números sería:

En el caso de 1 + 1 hemos indicado la situación del paso a la cifra inmediatamente superior mediante un 10.  Esto significa que el resultado de la operación es 0 y que arrastramos un 1 que añadimos ala siguiente.

En el caso de la sustracción o resta lo que se hace es añadir ceros al minuendo hasta que completa el número del sustraendo y acto seguido se lo invierte (es decir; se cambian los 0 por 1 y viceversa).

Finalmente, sumando el minuendo.

y el complemento del sustraendo se obtiene el resultado. Así, por ejemplo, para la suma de los números 243 y 89 tenemos: 243 = 11110011 y 89 = 1011001, Añadimos ceros a 89, quedando: 01011001, lo invertimos: 10100110, y sumamos; el resultado queda expresado numéricamente como sigue:

Lo mismo sucede en el sistema binario tanto con la multiplicación como con la división, siendo las operaciones mucho más fáciles y complicándose en el caso de números de muchas cifras, si bien es esto precisamente lo que no representa dificultad alguna para la máquina, ya que ésta no experimenta cansancio ni agotamiento y para ella el cálculo se reduce a verificar una serie de operaciones mecánicas.

En el caso de la multiplicación sólo cabe saber que

Sin necesidad de saber de memoria tabla de multiplicar  alguna. Así, por ejemplo, si queremos multiplicar los números 89 (1011001) y 41 (101001), los disponemos como es habitual y multiplicamos.

La operación resultante será

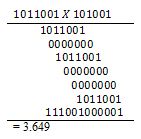
Finalmente, el caso de la división es, si cabe, todavía más ventajoso. No es necesario llevar a cabo comprobaciones engorrosas acerca   de la divisibilidad o no de un número por otro. O cabe una vez o no cabe, y con eso basta. Así, para la división de 39 (100111) por 13 (1101) tenemos que realizar la operación siguiente: