Tasa nominal, tasa efectiva y tasas equivalentes

La tasa convenida para una operación financiera es su tasa nominal. Tasa efectiva de interés es la que realmente actúa sobre el capital de la operación financiera.

La tasa nominal puede ser igual o distinta de la tasa efectiva y esto sólo depende de las condiciones convenidas para la operación.

Por ejemplo, si se presta un capital del 8% con capitalización trimestral, el 8% es la tasa nominal anual, la tasa efectiva queda expresada por los intereses que corresponden a $100 en un año, en las condiciones del préstamo. Para el monto, tenemos:

Tasas equivalentes. Son aquellas que, en condiciones diferentes, producen la misma tasa efectiva anual.

En el texto utilizaremos los siguientes símbolos para las diferentes tasas, expresadas en tanto por ciento.

i = efectiva anual j = nominal anual
m = número de capitalizaciones en el año

En la tabla 1, las columnas se refieren a las tasas en el período de capitalización. Así, para 12% con capitalización trimestral se tiene m = 4; j = 12; j/m = 12/4= 3%. El símbolo i en las tablas se refiere al tanto por uno, en el período.

Relación entre la tasa nominal y efectiva El monto de 1 al i efectivo anual es 1 + i. El monto de 1 ala tasa j por uno con m capitalizaciones en el año es (1 + j/m)m; la ecuación de equivalencia entre estos dos montos es:

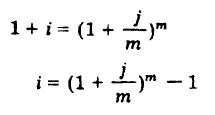
permite calcular la tasa efectiva equivalente a una tasa nominal j capitalizable m veces en el año despejando:

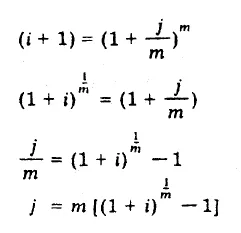
Introduciendo los nuevos símbolos, la fórmula del monto compuesto en n años para la tasa j capitalizable m veces en el año, queda:

número de períodos de capitalización en el año = m; número de años = n; número total de períodos = nin; tasa en el período = i = j/m

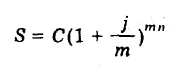
Para expresar la tasa nominal y el número de períodos de capitalización, se utiliza el símbolo j (m) que indica la tasa nominal j con m capitalizaciones en el año.

Fuente: Apunte de Matemáticas financieras de la UNIDEG