Teoría del Simplex
Se considera el programa lineal en su forma canónica Máx Z = cX
Sujeto a
Donde A es de orden m por n; cX son vectores renglón y columna respectivamente con n componentes y b es un vector columna con m componentes. Se denotan a las columnas de A por a1,a2,…,an con m < n.
Se considera a la matriz A partida en dos matrices, una B con m vectores linealmente independientes y otra n con n-m vectores linealmente dependientes:
Am,n = (Bm,m Nm,n-m)
La matriz B se le llamará la base y cualquier vector aj en A que no está en B, puede escribirse como una combinación de los vectores de b.
Es decir dado
Este puede escribirse como
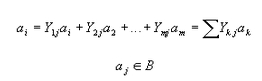
donde
i=1,…,m.
Se hace
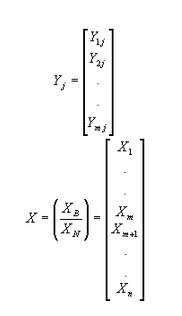
Por lo que y como B tiene inversa B-1, Yj = B-1 aj
Considerando las restricciones originales del programa lineal
AX = b
Se tiene que
donde
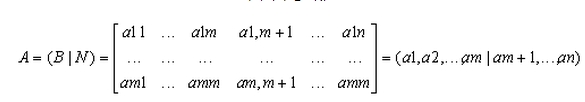
Entonces desarrollando se tiene
Si se hace uso de la definición de solución básica factible se tiene que
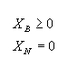
Y la desarrollada anteriormente se convierte en
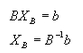
Que es una solución básica de 
El vector 
se le denomina vector básico 
y a , vector no básico. Si se parte el vector de costos o precios unitarios c en
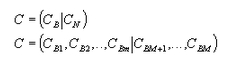
Se tiene que la función objetivo puede escribirse
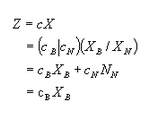
porque 
Fuente: Apunte de Investigación de Operaciones del Instituto Tecnológico de la Paz
