Sistemas de fuerzas paralelas

Sistemas paralelos son los constituidos por fuerzas cuyos vectores tienen la misma dirección, aunque pueden tener sentidos distintos.

Si {{Ai, Fi} ,i=1,..,número de fuerzas del sistema} es un sistema de fuerzas paralelas debe verificarse que:

FiΛF1=0 (i=2…,número de fuerzas del sistema)

La condición de paralelismo de la fuerzas es independiente de la ubicación de sus puntos (Ai} de aplicación.

Para un sistema de fuerzas paralelas siempre podemos definir un vector (g) que tenga la dirección común a todas las fuerzas de dicho sistema.

El vector g admite infinidad de definiciones, por ej.: puede coincidir con uno cualquiera de los vectores asociados a las fuerzas del sistema (g≡Fi), puede ser uno de los dos vectores de módulo unidad que son vectores directores de las rectas del sistema (g≡ F1/||F1||, ó g≡F1/||F1||), puede ser uno de los dos vectores cuyo módulo coincide con el valor medio de los módulos de los vectores del sistema, etc..

En función del vector director g las fuerzas del sistema se pueden representar de la siguiente manera:

{Ai, Fi=mi g}

Los escalares mi pueden obtenerse a partir de la siguiente expresión:

mi= (Fi.g) / (g.g)

Los coeficientes mi tienen la dimensión de una fuerza para el caso en que g sea un vector unitario (g≡ F1 / ||F1||), o ser adimensional cuando, por ejemplo, coincida con uno de los vectores asociados a las fuerzas del sistema (g≡ F1 ).

El torsor de un sistema de fuerzas paralelas representado con el polo de momentos en el origen (O) de coordenadas es:

τ={O={0,0,0}, R=(Σmi) g, M[O]=(Σmi(Ai-O))Λg}

Cuando no es nulo el vector resultante del sistema (R≠0 ⇔ Σmi≠0), la expresión del torsor de un sistema de vectores paralelos se simplifica al expresarlo en función de los parámetros que definimos a continuación:

µ ≡ Σmi = Σ((Fi.g) / (g.g)) = (R.g) / (g.g)
(G-O) ≡ Σmi(Ai-O) /µ

La expresión  introduce un punto singular (G) del sistema de fuerzas paralelas, de resultante no nula, al que denominamos centro del sistema de vectores paralelos, cuya ubicación es independiente de la definición del vector director g, (no ocurre lo mismo con la definición de µ), en efecto:

Σmi(Ai-O) /µ = (Σ(Fi.g) / (g.g))(Ai-O) / (Σ(Fi.g) / (g.g))

Σmi(Ai-O) /µ =(ΣFi.g) (Ai-O) / ΣFi.g

El vector g puede expresarse en función de uno de los dos vectores unitarios u directores de las rectas soporte de todas las fuerzas que componen el sistema, y por consiguiente, independientes de la definición de g:

g=±||g|| u

Sustituyendo la expresión en y simplificando la expresión resultante encontramos:

Σmi(Ai-O) /µ =(ΣFi.u) (Ai-O) / ΣFi.u

La representación del torsor del sistema paralelo, de resultante no nula, en (O)se puede escribir así:

{{0,0,0}, µ g, (G-O)∧µg}

y en el centro de vectores paralelos (G) del sistema:

{G, µ g,{0,0,0}}

La expresión  nos muestra que un sistema de vectores paralelos de resultante no nula tiene trinomio invariante nulo:

T=R.M[G]=µ g.0 = 0

También nos muestra que estos sistemas equivalen a una fuerza aplicada en G:

{G, µ g}

y que por consiguiente: la recta central de estos sistemas pasa por el punto G.

El centro de vectores paralelos no es atributo del torsor: sistemas de fuerzas paralelas equivalentes pueden definir centros de vectores paralelos diferentes, al tiempo que a todo sistema de fuerzas paralelas le corresponden infinitos sistemas equivalentes que no son sistemas paralelos.

Lo que si podemos afirmar es que todos los centros de vectores paralelos correspondientes a sistemas de fuerzas paralelas de resultante no nula y que a su vez son equivalentes, están situados sobre la recta central que es común a todos ellos.

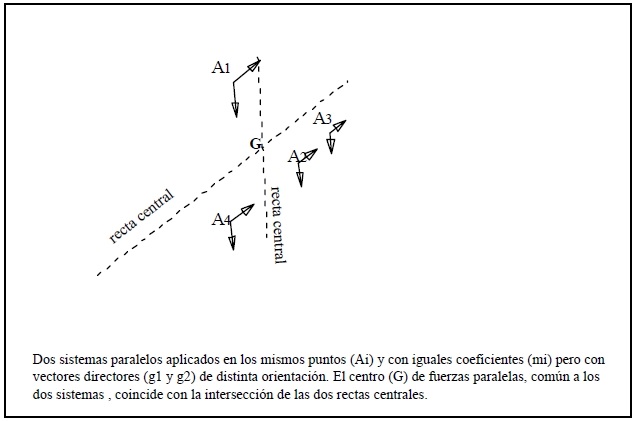
Si define un nuevo sistema de fuerzas paralelas que se obtiene, a partir de un primer sistema también paralelo y de resultante no nula, mediante una rotación común de todos los vectores asociados a dichas fuerzas alrededor de sus respectivos puntos de aplicación, el nuevo sistema tendrá el mismo centro que el primitivo, y su ubicación es la intersección de las correspondientes rectas centrales de los dos sistemas considerados.

La reducción a una fuerza {G, µ g} en la representación de los sistemas de fuerzas paralelas es la que aplicamos habitualmente a las fuerzas debidas a la gravidez, cuando actúan sobre un mismo sólido, en este caso, al centro de vectores paralelos lo denominamos centro de gravedad.

Esta reducción se puede extender a las distribuciones continuas de fuerzas paralelas derivadas o no de la gravidez.

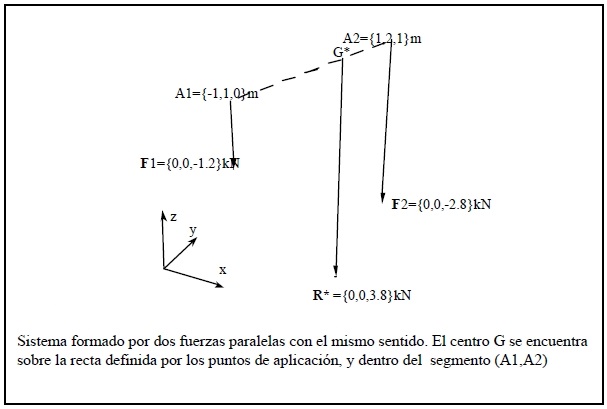
Para el caso de los sistemas de dos fuerzas paralelas con resultante no nula ({A1, F1},{A2, F2}, F1+F2≠0), si ambas tienen distinto sentido (m1 y m2 tienen distinto signo), el punto G se ubica sobre la recta que une A1 con A2 pero fuera del intervalo definido por estos dos puntos de aplicación y más cerca del punto de aplicación de la que tiene mayor módulo (figura 19); si F1 y F2 tuvieran el mismo sentido, G estaría ubicado dentro del segmento definido por los dos puntos de aplicación, también más próximo al punto de aplicación de la de mayor módulo.

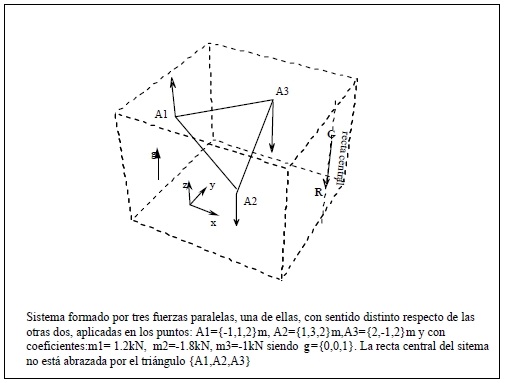
Análogamente podemos deducir limitaciones semejantes a la posición relativa de G respecto de los puntos de aplicación para los sistemas constituidos por tres fuerzas.

Fuente: Apuntes de Física del Departamento de Física Aplicada