El teorema (b) dice que todo sistema de fuerzas es equivalente a un sistema coplanario más un sistema de fuerzas paralelas cuya dirección fijamos arbitrariamente (teorema b) con la única excepción de que sea paralela al mencionado plano.
hipótesis
disponemos de:
– un torsor arbitrario: τ[O]={O, R, M[O]}
– un plano arbitrario: (P-A).n=0, donde P={x,y,z} representa al punto genérico del mismo, A es un punto conocido de este plano y n es un vector normal a dicho plano.
– un vector director v no paralelo al plano: v.n ≠ 0 demostración
Representación de las fuerzas
Al sistema paralelo le corresponde una resultante fc de dirección paralela al vector v (fc= β v ) por lo que su torsor será de la forma:
τc[A]={A, fc= β v , Mc[A]}
Al sistema coplanario que buscamos le corresponde el torsor:
τ’a[A]={A, f’a , M’a[A]=α’ n}
Sabemos que: (15.1) f’a. n=0
por tratarse de la resultante de un sistema coplanario y (15.2) Mc[A].v= 0
por tratarse del momento de un sistema de fuerzas paralelas al vector v.
La equivalencia entre el sistema original y la superposición de los sistemas buscados se expresa mediante las ecuaciones:
(15.3) f’a + fc = R Λ f’a + β v = R
(15,4) M’a[A]+Mc[A]=M[A] ⇔ α’ n+Mc[A]=M[A]
Siendo M[A] =M[O]+((O-B)ΛR
Para despejar el coeficiente β basta multiplicar escalarmente los dos miembros de la ecuación (15.3) por el vector n:
f’a.n + β v.n = R.n ⇒ β = (R.n) / (v.n )
fc = β v = (R.n) v / (v.n )
Para despejar el coeficiente α’ basta multiplicar escalarmente los dos miembros de la ecuación (15.4) por el vector v:
α’ n.v+Mc[A].v=M[A].v Λ α’ =(M[A].v) /(n.v)
M’a[A]=α’ n=(M[A].v) n /(n.v)
Para despejar el vector f’a podemos recurrir a la ecuación (3)
f’a = R – fc
Para despejar el vector Mc[A] podemos recurrir a la ecuación (4)
Mc[A]=M[A]-M’a[A]
Representación de las fuerzas
Si queremos una relación más directa entre estos últimos vectores y los datos iniciales podemos proceder de la siguiente manera: para despejar el vector f’a empezamos por multiplicar por la derecha los dos miembros de la ecuación (3) por el vector v
f’a ∧v+ β v∧v = R∧v ⇒ f’a ∧v = R∧v ,
y a continuación multiplicamos vectorialmente por la izquierda los dos miembros de el resultado obtenido en la operación anterior por el vector n
nΛ(f’a Λv) = nΛ((RΛv)
nΛ(f’a Λv) ≡ (n.v) f’a-(f’a .n) v=(n.v) f’a
f’a=(nΛ(RΛv)) / (n.v)
De forma análoga podemos proceder para despejar el momento Mc[A]: empezamos por multiplicar vectorialmente por la derecha los dos miembros de la ecuación (15.4) por el vector n
α’ nΛn+Mc[A]Λn=M[A]Λn Λ Mc[A]Λn=M[A]Λn
A continuación multiplicamos vectorialmente por la izquierda los dos miembros de esta última ecuación por el vector v
vΛ(Mc[A]Λn)=vΛ(M[A]Λn)
vΛ(Mc[A]Λn)≡(v.n) Mc[A] – (v. Mc[A]) n=(v.n) Mc[A]
Mc[A] =(vΛ(M[A]Λn)) / (v.n)
El sistema coplanario se puede reducir a una fuerza siempre que f’a ≠ 0 o lo que es lo mismo, si:
nΛ(RΛv)≠0
El sistema paralelo se puede reducir a una fuerza siempre que f’c ≠ 0 , es decir , si: R.n≠0
Representación de las fuerzas
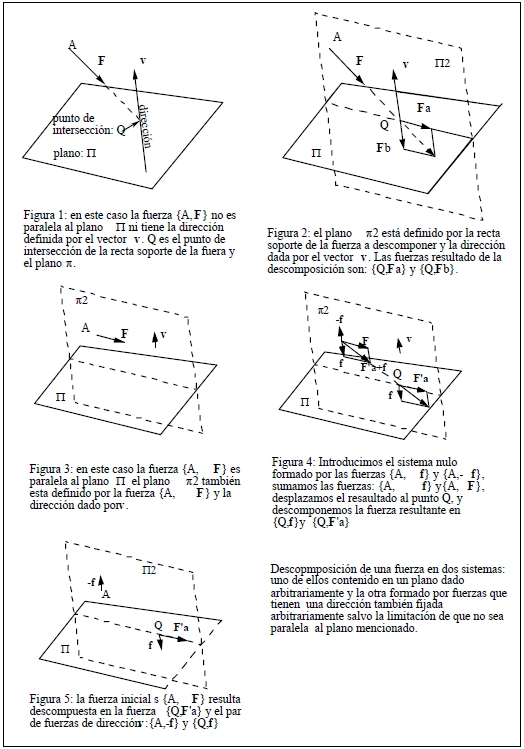
Fuente: Apuntes de Física del Departamento de Física Aplicada
