Las rectas soporte de un sistema formado por dos fuerzas con trinomio invariante no nulo se cruzan sin cortarse; este sistema no puede ser equivalente a una fuerza.
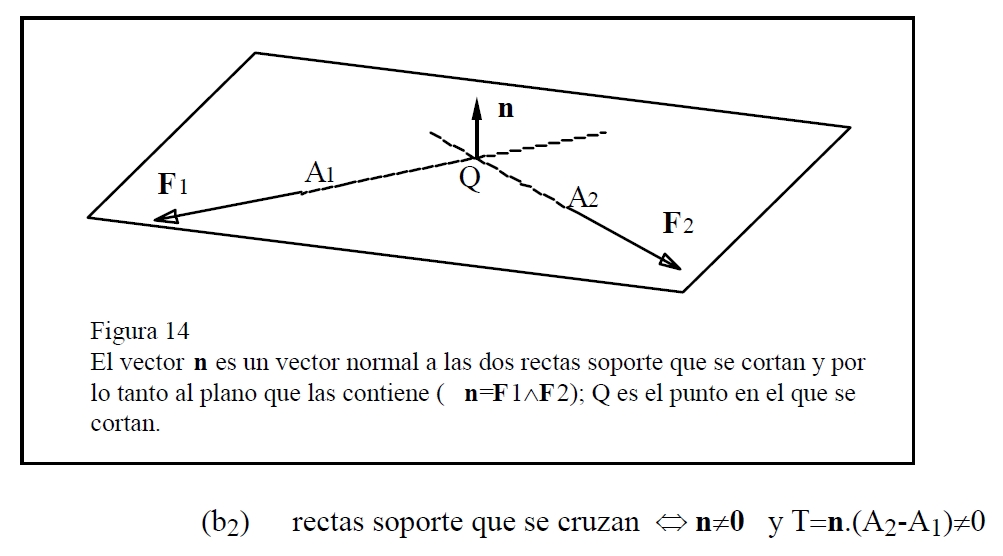
Sean A1 y A2 sus puntos de aplicación y F1 y F2 sus respectivos vectores asociados; vamos a demostrar que existen dos puntos Q1 y Q2 de sus respectivas rectas soporte tales que el vector (Q1-Q2) es perpendicular a las rectas soporte de ambas fuerzas, siendo el módulo de este vector la distancia entre ambas rectas siendo Q1=A1+λ1F1=A1- (F2.((A1-A2)Λn) F1/ (n.n),
Q2=A2+λ2F2=A2-( ( nΛ(A1-A2) ). F1) F2 / (n.n) y (Q1-Q2) = ( (A1-A2) . n ) n / (n.n).
Dado que no es nulo en este caso el trinomio invariante (T=(A2-A1).(F2ΛF1)=(A2-A1).n) los puntos Q1 y Q2 no coinciden.
demostración:
El no paralelismo de las fuerzas de vectores F1 y F2 se expresa por la condición:
(1) n ≡ F2 Λ F1 ≠ 0
La pertenencia del punto Q1 a la recta soporte de la primera fuerza se puede expresar de la siguiente manera:
(2) (Q1-A1) Λ F1 = 0 ⇔ (Q1-A1) = λ1 F1
Análogamente, por pertenecer a la segunda recta soporte, el punto Q2 verifica:
(3) (Q2-A2) Λ F2 = 0 ⇔ (Q2-A2) = λ2 F2
El vector (Q1-Q2) es perpendicular a las dos rectas soporte y por ello satisface las siguientes relaciones:
(4) (Q1-Q2) = µ n
De las expresiones: 2, 3 y 4 se deduce:(A1-A2)≡(A1-Q1)+(Q1-Q2) +(Q2-A2)= -λ1 F1 +µn + λ2 F2. Para despejar una de las incógnitas (λ1, µ y λ2) debemos multiplicar escalarmente ambos miembros de la igualdad anterior por un vector perpendicular a las otras dos, por ejemplo para despejar µ el vector a utilizar podría ser n (A1-A2).n =-λ1 F1.n +µn .n+ λ2 F2. .n= µn.n de donde se deduce : µ = ( (A1-A2) . n ) / (n.n) y (Q1-Q2) = ( (A1-A2) . n ) n / (n.n)
Para despejar el valor de la incógnita λ1 podemos multiplicar escalarmente los dos miembros de la mencionada igualdad por el vector η1=nΛF2
(A1-A2).η1 = -λ1 F1.η1 +µn .η1+ λ2 F2. .η1= -λ1 (F1.η1) de donde se deduce: λ1= – ((A1-A2).η1) / (F1.η1) y Q1=A1+ λ1 F1
Q1=A1- ((A1-A2).η1) F1/ (F1.η1)
F1.η1≡F1.nΛF2 =(F2 Λ F1).n=n.n
Q1=A1- ((A1-A2).(nΛF2)) F1/ (n.n) = A1- (F2.((A1-A2)Λn)F1/ (n.n)
Para despejar el valor de la incógnita λ2 podemos multiplicar escalarmente los dos miembros de la mencionada igualdad por el vector η2=nΛF1
(A1-A2).η2 = -λ1 F1.η2 +µn .η2+ λ2 F2. .η2= λ2 (F2.η2)
de donde se deduce: λ2= ((A1-A2).η2) / (F2.η2) y Q2=A2+ λ2 F2 Q2=A2+ ((A1-A2).η2) F2/ (F2.η 2)
F2.η2=F2.(nΛF1 )=-(n.n)
Q2=A2- ((A1-A2).(nΛF1)) F2/ (n.n) =A2- (F1.((A1-A2)Λn)F2/ (n.n)
que es lo mismo: Q1 = Q2. Esta última condición nos dice que las dos fuerzas son coplanarias siendo Q1 = Q2 su punto de intersección.
Fuente: Apuntes de Física del Departamento de Física Aplicada
