Dos fuerzas

Publicado en Representación de fuerzas

Se presentan las propiedades relativas a los sistemas formados por sólo dos fuerzas que representamos de la siguiente forma: {A1, F1} y {A2, F2}. Su torsor (τ) referido al polo A1 viene representado por:

τ={A1,R=F1+F2, M[A1]=(A2-A1)ΛF2 }
y su trinomio invariante (T=R.M[A1]) tiene por expresión: T=(A2-A1).(F2∧F1).

deducción:

T=R.M[A1]=F1.((A2-A1)ΛF2)+F2.((A2-A1)ΛF2)=F1.((A2-A1)ΛF2)

ya que es nulo el segundo de los productos mixtos del tercer miembro de la expresión anterior por tener dos factores iguales.

Permutando cíclicamente los factores del último producto mixto obtenemos: T=(A2-A1).(F2ΛF1) las rectas soporte de dos fuerzas pueden tener o no intersección.

La posición relativa de dos rectas se puede determinar a partir de los vectores: n=F2ΛF1 y (A2-A1).

(a) rectas soporte paralelas Λ n=0, que se subdividen en:
(a1) paralelas y distintas Λ n=0 y F1Λ (A2-A1)≠0
1

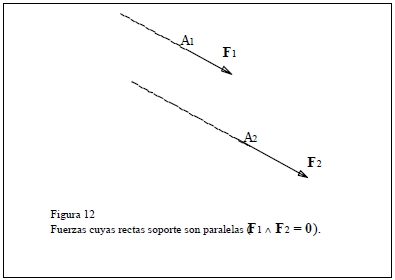
(a2) coincidentes Λ n=0 y F1Λ (A2-A1)=0

2

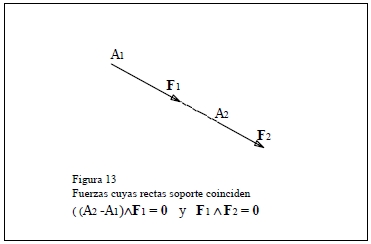
(b) rectas soporte no paralelas Λ n≠0, que se subdividen en:
(b1) rectas soporte que se cortan Λ n≠0 y n. (A2-A1)=0

3

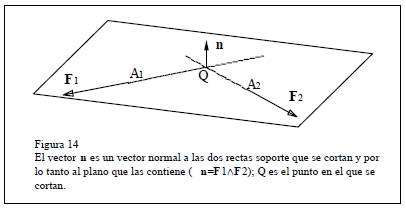
(b2) rectas soporte que se cruzan Λ n≠0 y Τ=n.(A2-A1)≠0

4

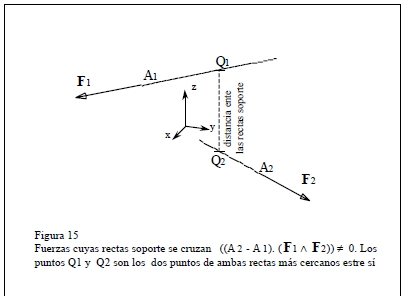
Fuente: Apuntes de Física del Departamento de Física Aplicada