Si se quiere reducir el sistema formado por las cuatro fuerzas {Pi , Fi} {i=1,..,4} representado en la figura 28.1.
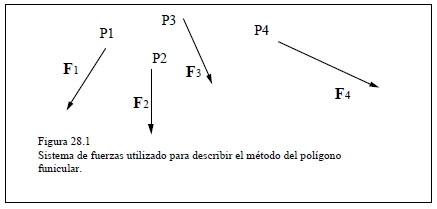
En primer lugar dibuja el polígono de estas fuerzas y que consiste en un sistema poligonal equipolente al anterior (figura 28.2) donde los lados del polígono corresponden a fuerzas equipolentes a las que
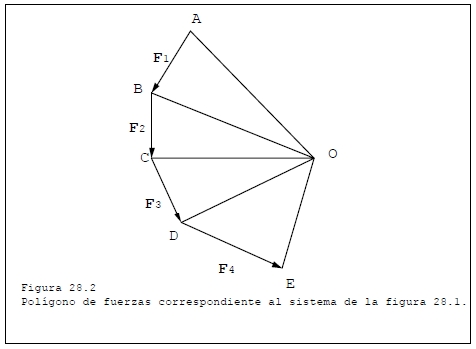
si se quiere reducir, pero tal que dichas fuerzas se dibujan de tal forma que el extremo de una coincida con el origen de la siguiente.
A continuación se elige un punto arbitrario (O) que nos servirá de polo y desde este último dibujamos los radios (OA, OB, OC, OD y OE) que conectan este polo con los vértices y los extremos del polígono de fuerzas.
La elección de otro polo aunque conducirá a un polígono funicular distinto no afectará al resultado de la reducción. Volvemos al sistema primitivo para dibujar el polígono funicular.
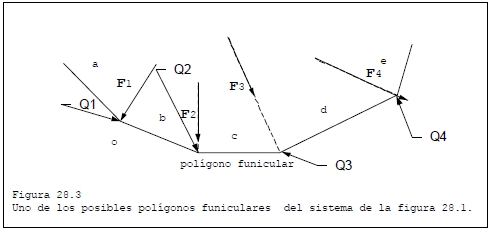
Desde un punto arbitrario (Q1) perteneciente la recta soporte de la primera de las fuerzas ({P1 , F1}) trazamos sendas rectas paralelas a los radios OA y OB representados en la figura 28.2. El punto Q2 es la intersección de la recta paralela al radio OB con la recta soporte de la fuerza {P2, F2}.
Desde este último punto trazamos una recta paralela al radio OC, la cual corta a la recta soporte de {P3,F3} en el punto Q3. Desde Q3 trazamos una recta paralela al radio OD que corta a la recta soporte de la fuerza {P4,F4} en el punto Q4. Por último trazamos una recta paralela al radio OE desde Q4.
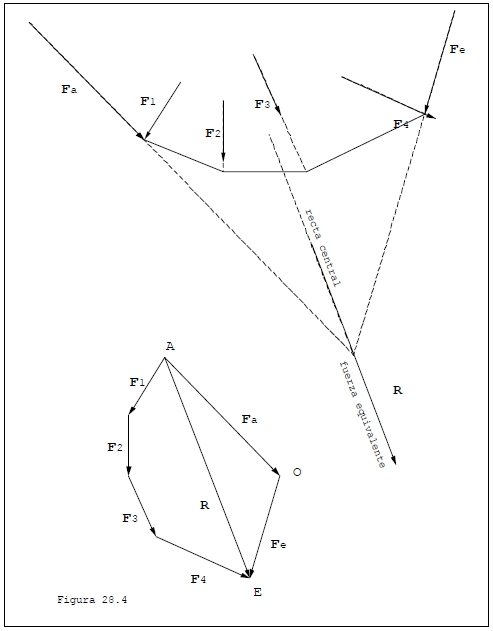
Es fácil demostrar que una fuerza de vector Fa representada en la figura 28.4 aplicada en el punto Q1 y una fuerza de vector Fe aplicada en el punto Q4 constituyen un sistema equivalente al inicial.
Para ello basta comprobar que la fuerza {P1, F1} es equivalente al sistema formado por las dos fuerzas: {Q1,Fa} y {Q1, (B-O)}, que la segunda fuerza {P2, F2} es equivalente al sistema formado por las dos fuerzas: {Q2,(O-B)} y {Q2, (C-O)}.
De manera análoga se encuentran las restantes equivalencias:{P3, F3} ≈ {Q3,(O-C)} y {Q3,(D-O)}, y que {P4, F4} ≈ {Q4,(O-D)} y {Q4,(E-O)}.
Se pueden comprobar que los sistemas:{{Q1, (B-O)} y {Q2,(O-B)}}, {{Q2, (C-O)}, {Q3,(O-C)}} y {{Q3, (D-O)} y {Q4,(O-D)}} son sistemas nulos.
Finalmente el sistema formado por las fuerzas {Q1, Fa} y {Q4, Fe}, equivale a una fuerza de vector R aplicada en el punto de intersección de las rectas soporte de las dos fuerzas mencionadas (Fig 28.4).
Al polígono funicular se le pueden imponer restricciones: que pase por dos y hasta por tres puntos dados, que pase por un punto y que la recta soporte de su último lado tenga una determinada dirección, etc.
El método del polígono funicular permite, entre otras posibilidades, diseñar arcos que trabajan a compresión, por ejemplo los arcos construidos con dovelas y predecir la configuración de los cables ligeros sometidos a cargas puntuales.
Fuente: Apuntes de Física del Departamento de Física Aplicada
