Denominamos resultante de un sistema de fuerzas puntuales o deslizantes {Ai, Fi , i=1,2,…,n) al vector que resulta de sumar los vectores asociados a todas las fuerzas de dicho sistema:
resultante ≡R≡Σi (Fi)
El momento resultante de un sistema respecto del polo Q es la suma de los momentos de todas las fuerzas que componen el sistema respecto de este punto:
momento resultante respecto del polo Q: M[Q] ≡Σi ((Ai -Q)ΛFi )≡ Σi Mi[Q]
El efecto del cambio de polo en el momento resultante de un sistema viene reflejado por la siguiente expresión:
M[Q1] = M[Q]+(Q-Q1)ΛR
En efecto:
M[Q1] ≡Σi ((Ai- Q1)ΛFi)=Σi(((Ai–Q)+(Q-Q1))ΛFi)= M[Q1] =Σi((Ai–Q)ΛFi)+(Q-Q1)∧Σi (Fi)≡ M[Q]+(Q-Q1)ΛR
La relación de equivalencia entre sistemas de fuerzas puntuales se extiende a los sistemas de fuerzas deslizantes. Decimos que dos sistemas de fuerzas son equivalentes, cuando tienen la misma resultante y en relación al mismo punto (polo de momentos), tienen el mismo momento resultante.
La figura nos muestra como varía el momento resultante, de un sistema de fuerzas con vector resultante no nulo, en relación a la ubicación del polo, en ella puede verse que si los polos se alinean según una recta paralela a la resultante el vector momento resultante del sistema no varía.
Demostración
Si (Q1 -Q2)ΛR=0 Λ M[Q1]=M[Q2]+(Q1 -Q2)ΛR=M[Q2]
Si dos polos no están alineados en la dirección de la resultante ((Q1 -Q2)ΛR≠0), los correspondientes momentos resultantes serán distintos.
Demostración
Si (Q1 -Q2)ΛR≠0 Λ M[Q1]=M[Q2]+(Q1 -Q2)ΛR≠M[Q2]
Observen en la figura la presencia de un recta también orientada en la dirección de la resultante, para la cual el vector momento resultante del sistema respecto de sus puntos tiene la dirección de dicha recta, a esta recta se la denomina recta central del sistema y la trataremos más adelante.
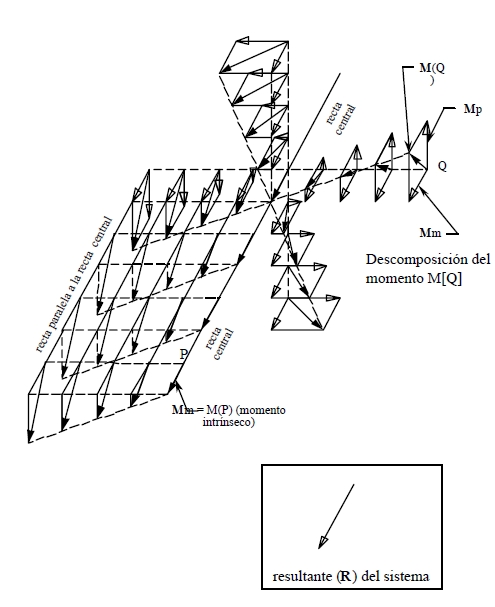
Fuente: Apuntes de Física del Departamento de Física Aplicada
